Substantially reducing noise costs of jet skis requires banning them
from most waters, and mandating that they stay at least a
quarter-mile from shore at remaining areas.
APRIL 2000
“Jet Ski” is a registered trademark of Kawasaki Motors Corp., U.S.A. In this report we use “jet ski” (in lower case) to denote a generic class of watercraft that is popularly known and commonly referred to by that term. We do not mean to single out Kawasaki for criticism, nor do we assert or imply that Kawasaki’s products are noisier than those of their competitors.
The term “personal watercraft” is often used interchangeably with “jet ski,” particularly in legal and regulatory contexts. However, “personal watercraft” is in some respects a misnomer, since jet skis increasingly are designed to carry two or more people. In addition, many non-motorized craft usable by one person, such as kayaks, canoes, small rowing shells and windsurfers could (perhaps even more aptly) be characterized as personal watercraft. (Note that “windsurfer,” which we use generically here, is also a trademark when capitalized.) Another term seen in this context, “thrill craft,” is inappropriate for this report because it includes other ultra-fast boats.
The term “jet ski” in its generic sense is firmly established in popular usage. See, for example, Time magazine (June 14, 1999), the New York Times (Sept. 16, 1998), and LakeLine magazine (June 1994), among many others. In the New York Times article cited, it was noted that personal watercraft are “commonly known as jet skis,” and that term was used in the headline. We continue in that vernacular tradition.
DROWNING IN NOISE 1
Context. People don’t like noise and will pay to avoid it; witness the reduced market value of houses near airport runways and highways. In this report, we estimate, in quantitative terms, just how annoyed beachgoers in the United States are by the sound of jet skis(1) operated nearby.
We do this through a quantitative model that estimates the monetary value of the “disamenity” (lost enjoyment) that jet ski noise introduces into beach environments in America. Our results, expressed in dollars, are what beachgoers would pay to rid lake, bay, river and ocean beaches of jet ski noise — if there were an entity that would take their money and turn off the noise.
We present two types of estimates: the “annoyance” cost of jet ski noise itself, and the effectiveness of possible strategies to reduce this cost. Other social and environmental costs of jet skis, such as water and air pollution, harm to swimmers and wildlife, etc., are discussed in Section 9, but only summarily; our subject here is jet ski noise and its cost to beachgoers.
Estimates of Jet Ski Noise Costs
National jet ski noise costs: The 1.3 million jet skis in the
United States impose approximately $900 million of noise costs on U.S.
beachgoers each year.(2)
Noise costs per jet ski: The average jet ski imposes $47 of noise pollution costs on beachgoers in the course of a day’s use. Since the average jet ski is used 15 days a year, it imposes approximately $700 of noise costs on beachgoers each year.
Future growth in jet ski noise costs: With the number of jet skis in use growing by 100,000 a year, the total noise cost will continue to increase. Even if all jet skis sold after 2000 are substantially quieter (by 5 decibels) than current models, jet ski noise costs to beachgoers nationwide in 2005 will be approximately $1.07 billion, or 18 percent greater than the year-2000 total.
These figures do not include the noise costs (including reduced property values) to residents of waterfront areas in range of jet ski noise, or to canoeists, kayakers and other boaters, or to hikers on nearby trails. (These are noted separately on pp. 6-7.)
DROWNING IN NOISE 2
Table 1: Noise Cost to Beachgoers per Day from One Jet Ski
| Beach Type | Number of Beachgoers | Highest Cost to Any Beachgoer | Average Cost to All Beachgoers | Total Cost to All Beachgoers |
| Secluded Lake | 2-3 | $8.83 | $7.02 | $15 |
| Intermediate Lake | 22 | $5.02 | $3.13 | $69 |
| Popular Lake | 220 | $1.52 | $0.76 | $167 |
| Secluded Ocean | 13-14 | $1.95 | $1.20 | $16 |
| Intermediate Ocean | 137 | $1.74 | $0.80 | $109 |
| Popular Ocean | 1375 | $0.96 | $0.39 | $538 |
Beach types are defined in Table 3 on p. 34.
Jet ski noise costs by beach type: We define beaches as popular, secluded or intermediate-use, based on beach-user population density; and also divide them into “lake-type” beaches (a category that also includes beaches along bays, rivers and canals) or ocean beaches. As Table 1 shows, jet ski noise costs per beachgoer are highest at secluded lakes. On the other hand, noise costs per jet ski are highest at popular beaches, since more people are affected.
Table 2: National Jet Ski Noise Costs to Beachgoers, per Year
| Beach Type | Share of Jet Ski Use | Total Beachgoer Noise
Costs From Jet Skis |
Share of Total Cost |
| Secluded Lakes | 55.2% | $110 million | 12% |
| Intermediate Lakes | 18.4% | $171 million | 19% |
| Popular Lakes | 18.4% | $451 million | 50% |
| Secluded Oceans | 4.8% | $12 million | 1% |
| Intermediate Oceans | 1.6% | $27 million | 3% |
| Popular Oceans | 1.6% | $136 million | 15% |
| Total Beachgoer Noise Cost from Jet Skis, per year: $908 million |
Figures in table are derived in Section 6.
According to industry surveys, some 92% of jet ski usage is on lake-type waters, with the remaining 8% on oceans. We assume that 60% of usage is on secluded waters, while the other 40% is split equally between intermediate-use and popular water bodies. With these assumptions, the total national noise cost to beachgoers from jet skis is
DROWNING IN NOISE 3
just over $900 million a year. As Table 2 shows, roughly half of the total is experienced on popular lakes, one-fifth is on intermediate lakes, 15% is on popular ocean beaches, and 12% is on secluded lakes. All lake-type beaches (lakes, bays, rivers and canals) bear $732 million in jet ski noise costs, or 81% of the total.
Why Jet Ski Noise Is So Annoying. Jet ski noise is different from that of motorboats. The heart of the difference, and the crux of the jet ski noise problem, is that jet skis continually leave the water. This magnifies their noise impact in two ways.
First, minus the muffling effect of the water, the jet ski engine’s exhaust is much louder, typically by 15 dBA. As a result, an airborne jet ski has the same noise impact on a listener at the water’s edge as an in-water jet ski 8 times closer, or the same as 32 identical in-water jet skis at the same distance.
Second, each time the jet ski re-enters the water, it smacks the surface with an explosive “whomp” — sometimes with a series of them.
Leaving the water is central to the fun of jet skiing; for many jet skiers, the ultimate thrill is to take to the air and bounce off the water repeatedly. But jet skis don’t have to deliberately jump to leave the water. Because of the short hull, a jet ski ridden fast on even a slightly choppy surface will lift out of the water naturally, eliminating the water’s sound-muffling action and creating that jarring whomp.
And that’s not all. The direct noise-amplifying effect of leaving and re-entering the water is compounded by the variable nature of the noise. Rapidly varying noise is much more annoying than constant noise, as decades of psycho-acoustics research have established. A varying noise commands the hearer’s continuous attention, making it especially bothersome. This phenomenon has been largely overlooked in the jet ski controversy. We have quantified its effect here, enabling us to capture the full and unique impact of jet ski noise.
Strategies to Reduce Noise Costs. Three broad approaches have been suggested to reduce jet ski noise costs to beachgoers:
DROWNING IN NOISE 4
|
Key Results |
|
Today (year 2000) Number of jet skis in America: 1,300,000
Future (year 2005) Number of jet skis in America: 1,800,000
Mitigation strategies (% reductions are from current $908,000,000 cost to beachgoers)
|
DROWNING IN NOISE 5
We have found that only the third approach — restricting usage — holds real promise for significantly reducing jet ski noise costs in a region or nationwide. (Banning “wake-jumping” is infeasible; see Section 8. Taxing users for jet skis’ environmental damage is discussed further below. “Temporal segregation” is treated briefly in Section 8.)
We estimated the measures necessary to reduce nationwide jet ski noise costs to beachgoers by three-fourths from today’s levels by the year 2005, while assuming that the number of jet skis in use will rise from 1.3 million to 1.8 million. Meeting this goal would require banning jet skis from 90% of all U.S. lakes, bays, rivers and oceans.
Alternatively, the same objective can be met by banning jet skis from 82% of waters, and requiring jet skis at the remaining sites to operate at least a quarter-mile from shore. (If the half a million jet skis projected to be purchased between now and 2005 are 5 decibels quieter than current models, on average, then the 82%-complete ban could be relaxed slightly, to a level of 78%.)
By themselves, “minimum-distance” laws will not cure the problem of jet ski noise to beachgoers. We estimate that barring jet skis from operating within 500 feet of shore would reduce nationwide noise costs from current jet skis by only 27%; moreover, this improvement would be wiped out by growth in usage in five years. Even a quarter-mile rule would only reduce current jet ski noise costs by 48%, and by 2005 this reduction would be trimmed to 28%.
Perhaps surprisingly, the introduction of quieter models will not reduce total jet ski noise costs at all. Even if every new jet ski sold after 2000 were built with modified engine designs that some manufacturers claim reduce noise emissions by 5 decibels, the national jet ski noise cost to beachgoers in 2005 would still be 18% greater than today, according to our calculations. Because they apply to new models and not to jet skis currently in use, technological refinements to make jet skis quieter will not lessen the absolute burden to beachgoers, nor even prevent that burden from growing.
Taxes on jet ski noise: Another approach to reducing jet ski noise costs is to “internalize” them by taxing their sale or use. We estimate that a tax rate corresponding to just half of a typical jet ski’s noise costs would drive up the purchase or rental price to an extent that a third of all jet ski use — and noise — would be eliminated. Higher
DROWNING IN NOISE 6
taxes capturing a larger share of jet ski noise costs, as well as their pollution and injury damage to humans, wildlife and marine ecosystems, would eliminate larger fractions of jet ski use and noise.

Substantially reducing noise costs of jet skis
requires banning them
from most waters, and mandating that they stay at least a
quarter-mile from shore at remaining areas.
Jet Ski Costs Apart From Beachgoers
Non-beachgoer noise costs: Using the framework developed here to estimate jet ski noise costs to beachgoers, but employing rougher estimates for some key parameters, we have estimated that jet ski noise costs to owners of waterfront property in the U.S. are on the order of $230 million a year; similarly, jet ski noise costs to non-motorized boaters (e.g., canoeists, kayakers, and windsurfers) are on the order of $120 million annually. These figures are not included in the noise costs to beachgoers given above.
Other costs of jet skis: After reviewing the literature on both jet ski emissions and the health costs of air pollution, we have estimated that air pollution from jet skis imposes at least $240 million a year in health costs to Americans. Other costs from jet skis, including
DROWNING IN NOISE 7
pollution of marine environments, habitat and wildlife destruction, and endangerment and injury to humans, are mentioned but not quantified later in this report. These costs are treated in Section 9.
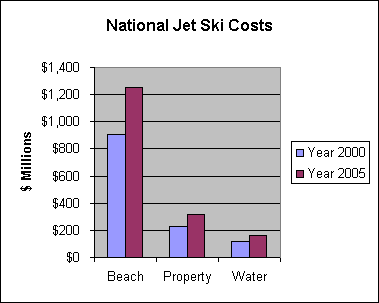
National jet ski noise costs to beachgoers are now
over $900 million
and could reach $1.25 billion in 2005 (see Section 6). Noise costs
to property owners and water recreationists are estimated roughly
in Section 9.
DROWNING IN NOISE 8
This report is addressed to policymakers, resource economists and, above all, the many people throughout the United States whose pursuit of happiness at our nation’s shorelines and beaches is diminished or made impossible by noise from jet skis.
DROWNING IN NOISE presents a novel approach to the issue of jet ski noise. The authors and publisher hope it will prove to be a powerful tool in encouraging jurisdictions to act against the enormous and growing vexation of jet ski noise.
The centerpiece of this report is a model that quantifies how much beachgoers are being made to sacrifice their own pleasure and well-being because of noise from jet skis. The model estimates the total amount of jet ski noise to which people at a beach are subjected, and then translates their displeasure due to this noise into dollars. The resulting dollar total expresses how much, and how often, noise from jet skis degrades an experience treasured by most Americans: a day at the beach.
Translating noise into dollars of “disamenity”(3) is not new, although DROWNING IN NOISE is the first noise-cost analysis of jet skis, to our knowledge. Still, quantifying the cost of noise is not a widely familiar concept. Our approach is based on the idea that the value that people derive from recreational activities (like visiting a beach) can be estimated, using measurable factors such as the amount of money that they spend getting there, as well as survey data on the value of beach recreation. To calculate how much the value of “beachgoing” is degraded by jet ski noise, we draw on studies that have measured the effect of environmental noise on residential property values.
When empirical values are fed in — the jet ski is so many feet offshore, it is so many decibels loud at the source, the beach is so many feet wide and deep, the beach is “popular” or “secluded” with a corresponding background noise level, the average beachgoer spends so many dollars to be at the beach — the model yields estimates of the value of people’s time at the beach, the additional decibels of jet ski noise to which the beachgoers are exposed, and the dollar value (the cost to them) of their reduced pleasure of being at the beach.
To be sure, all these variables differ over a wide range — no two beachgoers are exactly alike, or occupy the same position on the
DROWNING IN NOISE 9
beach, or are equally sensitive to noise; no two jet skis make the same noise or operate at a uniform distance from the beach; and so forth. Accordingly, the jet ski noise model incorporates random elements, so that the variables may encompass a range of plausible conditions.
|
Curing the Noise Problem |
|
This report finds that the only way to reduce noise annoyance costs to beachgoers from jet skis significantly — either regionally or nationally — is to concentrate usage in a few designated areas. Restricting usage to 10% of U.S. waters would reduce the national noise cost to beachgoers by 82% (possibly by more, if jet ski usage declined as a result). By 2005, the reduction in noise cost from this policy would shrink to 75%, if usage continued to grow at the present rate in spite of the restriction. A consequence of this strategy would be a near-doubling in noise costs at areas where jet skis would be permitted, as users congregated there, unless overall usage did in fact diminish. A second approach would forbid operation of jet skis near shore (except en route to or from a launch area, and then only within strict speed limits) This approach, unfortunately, has limited value, because sound carries extremely well across open water. Keeping jet skis at least 500 feet from all beaches would eliminate only 27% of noise costs to beachgoers in 2000; by 2005, with a projected 38% increase in the number of jet skis, total noise costs with a 500-foot rule would be 1% higher than today. Even a quarter-mile ban would only reduce current jet ski noise costs by 48%, and by 2005 this reduction would be trimmed to 28%. Reducing jet ski engine noise will accomplish even less, due to the slow scrappage rate of current machines. Even if all new models were 5 dBA quieter than present jet skis —which appears to be the outer limit of improvements touted by some manufacturers — national jet ski noise costs in 2005 would be 18% higher than in 2000. To keep the year-2005 noise costs at today’s levels while total usage grows, the 5 dBA improvement would need to be made on 65% of all existing machines (as well as on all new ones), which is infeasible technically, let alone politically. The most powerful approach is to combine the three mitigation strategies. We estimate that limiting usage to 10% of U.S. waters, and restricting operation there to at least a quarter-mile from beaches, would eliminate 88% of noise costs to beachgoers nationwide. Maintaining these restrictions while requiring all new jet skis to be 5 dBA quieter would yield an 85% reduction in national noise costs in 2005 compared to today’s level, even if the number of machines in use continues to grow at the present rate. |
DROWNING IN NOISE 10
The model then repeats, many times, its calculations of excess noise and its cost. The averages of these “iterations” are statistically superior to the result of merely multiplying a series of average values.
The model can be run in this way for particular real-world beaches or for idealized “types” of beaches (e.g., a “popular lake”). The resulting estimates of jet ski noise costs are often large — large enough that hitherto passive regulators and legislators might be made to take notice. For a typical popular lake beach, the noise from a single jet ski operating close to shore for a few hours robs the collective beachgoers of a hundred dollars in lost enjoyment for the day. For the nation as a whole, we estimate that the noise annoyance costs of jet skis to all U.S. beachgoers over the course of a year is slightly over 900 million dollars.
These may seem large costs to associate with what is often considered a mere “nuisance.” But jet skis are now ubiquitous in America — an estimated 1.2 million were in use in 1999, with 1.3 million expected to be operating in 2000, the “base year” for this report. And beachgoing is an enormously popular and valued activity. The $900 million annual cost of jet ski noise is the sum of the costs from close to a billion individual occasions of “disamenity” — almost a billion beach-days marred, or ruined altogether, by the roar and whine of a jet ski.
Our estimates of the average noise cost imposed by one jet ski on each of these occasions reflect the wide variations in beach environments and users, and range from around 40 cents per beachgoer on a noisy ocean beach, to seven dollars per visitor to a quiet lake shore. While there is necessarily an element of judgment in many of the underlying assumptions, both the model and our valuations of its parameters are rooted in the literature of acoustics, economics and mathematics. If our aggregate estimate of jet ski noise costs seems large, that is the consequence of turning thousands of formerly tranquil waters into aquatic go-cart tracks.
DROWNING IN NOISE was undertaken to make these costs clear and comparable to other social costs. That a lone jet ski operating near shore for just a few hours can disturb hundreds of people along the beach is widely understood. That the aggregate costs associated with these same disturbances can reach a hundred dollars or more gives this understanding greater concreteness.
DROWNING IN NOISE 11
In a very real sense, the tribute of “disamenity” extracted by jet ski users from everyone else in earshot is a kind of robbery. With the full extent of the cost now apparent, regulatory and legislative actions — usage restrictions, stringent equipment standards, perhaps noise taxes — should follow.
The Noise Pollution Clearinghouse and the authors of DROWNING IN NOISE stand ready to help individuals, advocacy groups and government agencies evaluate jet ski noise costs and take action to minimize and eliminate them. We hope that DROWNING IN NOISE will stimulate specific analyses of jet ski noise costs at shorelines of concern, as well as assessments of other noise annoyance costs.
|
Decibel Levels and Differences |
|
Consider a noise source that is 60 decibels loud to a person at a certain location (e.g., on a street or beach). What is the effect of the noise source becoming 10 dBA louder (to 70 decibels)? Subjectively it means that the source now sounds, or feels, twice as loud (see sidebar on p. 16). In terms of physics, however, it means that the noise source is now 10 times more energetic. What could make the noise 10 dBA louder? One way would be if the single noise source was augmented by 9 identical sources (for a total of 10) at the same distance as the first. Another would be if the noise source moved 4 times closer to the listener, i.e., if the distance to the source was reduced by three-fourths (assuming the listener and the source are separated by water). Conversely, making the noise source 10 dBA quieter means that it now feels half as loud as before. This requires reducing the power from the noise 10-fold, which can be accomplished either by removing nine-tenths of the noise sources (if the noise was emanating from a large number of identical sources), or moving the source(s) 4 times further away. The table of standard noise levels on p. 14 may help the reader gauge the subjective loudness of various decibel levels, as well as the effect of 10 dBA increases or decreases in noise levels. |
DROWNING IN NOISE 12
Less than two decades since they were introduced, jet skis have become ubiquitous on U.S. waterways. Sales of jet skis currently run at around 150,000 a year; older models are being scrapped at only a third of that rate, and an estimated 1.3 million “personal watercraft” are now operating on the nation’s bays, lakes, rivers and oceans.
In reaction to the nearly constant intrusion of jet ski noise on thousands of beaches and shorelines, organizations of anglers, canoeists, nature-lovers and beachgoers have campaigned strenuously to limit jet ski use. Prodding by national and local citizens’ groups has resulted in the banning of jet skis from more than two dozen units of the National Park Service, including Yellowstone, Everglades and Grand Canyon National Parks, and from dozens of prized lakes from Lake Tahoe in the Sierra Nevada range to the Stockbridge Bowl in western Massachusetts.(4)
Vermont now bans jet skis from lakes and ponds smaller than 300 acres, effectively limiting them to lakes at least a half-mile across,(5) and the machines have been barred from waterways of the San Juan Islands of Washington State and of Marin County, north of San Francisco. Some jurisdictions, including San Francisco County and south Florida’s Monroe County, require jet skis to keep a considerable distance — in some instances, almost a quarter-mile — from shore.(6)
Yet bans or operating limits are still exceptional. Restrictions have been adopted piecemeal, and only over bitter resistance by jet ski manufacturers and user groups. For the most part, following America’s laissez-faire tradition toward motorized recreation, jet skis have been permitted to proliferate, almost as-of-right, while objectors must bear the burden of proving harm and seeking redress. Throughout the 1990s, in fact, while citizens were scrambling to marshal facts and mount grassroots campaigns, the jet ski industry and user groups were cultivating influence and entering mainstream culture.
Manufacturers and users insist that jet ski noise is little different from noise generated by other motorized watercraft.(7) But their arguments appear to ignore fundamental differences between jet skis and motorboats. While jet skis can sometimes be observed operating no more loudly than motorboats, as a general rule jet skis are considerably noisier and more disturbing. Three differences stand out:
DROWNING IN NOISE 13
1. Jet skis are designed and used differently from motorboats, in ways that typically make them far more annoying to other people in the same environment.
With their small size and shallow draft, jet skis can venture closer to shore than motorboats. Moreover, whereas motorboats are used for many different reasons, from excitement to relaxation, jet skis are designed and marketed for only one reason: the thrill of speed. Jet skis are not used for fishing or cruising; a jet ski is seldom driven at
|
Origin of this Report |
|
This report originated during a late-summer outing several years ago. My family and I were hiking on a trail along the Hudson River, north of New York City. We stopped to picnic at a rock overlook high above the water. The broad river stretched for miles below us, and the air shimmered in silence, punctuated by the happy murmurs of our two-year-old. Then two jet skis came roaring up the river. They spun round and round, crashing over each other’s wakes again and again. We were a thousand feet up and half a mile back from the river, but the jet skis resounded like chainsaws. We had escaped the city, braved the hot sun and struggled against gravity, only to find ourselves trapped in somebody else’s idea of fun. It occurred to me … if we, remote though we were, were nevertheless caught in the jet skis’ noise field, so must be many others, on the mountain or along the shore. There had to be a way, using acoustics and geometry, to calculate the volume of noise being showered on each of us. Could there also be a way to estimate the cost of that noise? From my work in transportation policy, I knew there was an extensive literature correlating noise from highways and airports with reduced home values. Several studies had derived a decibel-dollar relationship, associating each extra decibel with a certain percentage loss in the sale price of houses. One could apply this to calculate the dollar loss in amenity for each person subjected to jet ski noise. I described the problem to Howard, a math and computer science professor with a multidisciplinary background including physics and acoustics, and a lifelong friend since grade school. In a series of e-mails we specified the problem (transferring it from a riverbank to a beach) and began outlining an analytical approach. In due course we contacted the Noise Pollution Clearinghouse, which commissioned this report. — Charles Komanoff |
DROWNING IN NOISE 14
less than full throttle. Motorboaters as often as not head for a fishing or picnicking spot, then douse the engine when they get there. But jet skiers seldom have a destination in mind. Rather, they use their vehicles continuously as a recreational end in themselves.
2. The heart of the difference between jet skis and motorboats, and the crux of the jet ski noise problem, is that jet skis continually leave the water. This magnifies the noise in two ways. First, without the muffling effect of the water, the engine’s exhaust is much louder — typically by 15 dBA; an airborne jet ski has the same noise impact on a listener at the water’s edge as an in-water jet ski 8 times closer, or the same as 32 identical in-water jet skis at the same distance. Second, each time the jet ski re-enters the water, it smacks against the surface with an explosive “whomp” — sometimes with a series of them.
Leaving the water is central to the fun of jet skiing. For many jet skiers, the ultimate thrill is to take to the air and bounce off the water repeatedly. This is easily accomplished — by jumping the wake from a passing motorboat, or from another jet ski (often in a duet of mutual wake creation and riding), or from one’s own machine. But jet skis don’t have to deliberately jump to leave the water: because of the short hull, a jet ski ridden fast on even a slightly choppy surface will lift out of the water naturally, eliminating the water’s sound-muffling action and creating the jarring whomp.
Noise Levels of Common Sources (Cowan, 1994)
| Sound Source | dBA |
| Air raid siren at 50 ft | 120 |
| Maximum levels in audience at rock concerts | 110 |
| On platform by passing subway train | 100 |
| On sidewalk by passing heavy truck or bus | 90 |
| On sidewalk by typical highway | 80 |
| On sidewalk by passing automobiles with mufflers | 70 |
| Typical urban area background / busy office | 60 |
| Typical suburban area background | 50 |
| Quiet suburban area at night | 40 |
| Typical rural area at night | 30 |
| Isolated broadcast studio | 20 |
| Audiometric (hearing testing) booth | 10 |
| Threshold of hearing (person w/o hearing damage) | 0 |
DROWNING IN NOISE 15
So whether by the operator’s intent or the vehicle’s design or both, jet skis wind up “out of the water” much of the time — certainly far more than all but the occasional (and also annoying) “cigarette” boat to which jet skis are sometimes likened. And not only does this raise the jet ski’s instantaneous noise emission by a very considerable 15 dBA on average; the effect is vastly compounded by the variable nature of the noise.
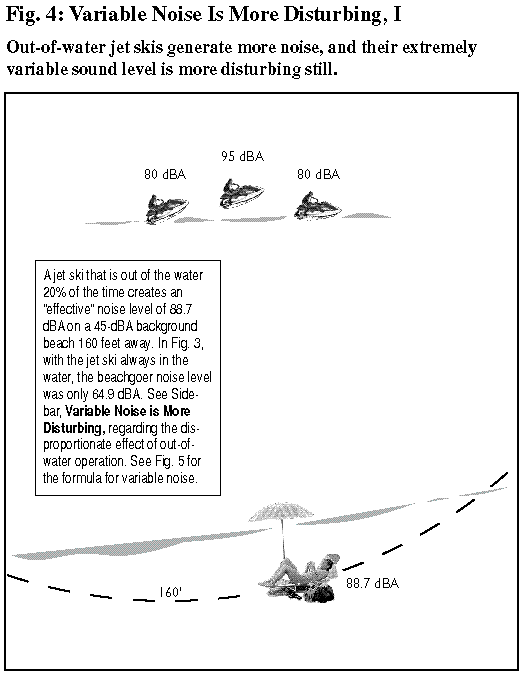
An established finding of psycho-acoustics is that rapidly varying noise is much more annoying than constant noise — even a constant noise that is equal in intensity to the loudest instantaneous noise in a series. This is a truth known by experience to anyone who has been repeatedly startled or disturbed by a loud but intermittent sound, like a jackhammer at a construction site. A varying noise commands the hearer’s continuous attention, making it especially bothersome. This ensures that jet skis’ whirring and whomping noises, varying from moment to moment, will be much more annoying than the relatively constant sounds produced by other watercraft. (For quantification of this annoyance, see sidebar, “Variable Noise is More Disturbing,” on p. 21.)
3. The final characteristic that distinguishes jet skis from motorboats is their rapid maneuvering and frequent speed changes. In addition to jumping wakes, jet skis are designed and marketed for weaving, sharp turning, spinning doughnuts and generally erratic throttle use. As a result of these maneuvers, the jet impeller has no consistent water “throughput,” and thus, no consistent load on the engine. Consequently, the engine’s speed rises and falls from moment to moment with each maneuver. The result is a penetrating whining sound, rising and falling rapidly in pitch like a dentist’s drill and demanding the attention of anyone within earshot.(8)
We estimate that jet skis are operating “out of the water” or in the rapid maneuvers just described, around 20% of the time. Both involve not only elevated noise emission levels but also varying — hence, unusually annoying — sounds.
DROWNING IN NOISE 16
|
The Mathematics of Decibels |
|
In its simplest form, noise level is measured either as pressure (P, in pascals) or as power flux (E, in watts per square meter). In practice, however, the usual unit of measure is the decibel (dB, or a widely used version called dBA calibrated to the sensitivity of the human ear). Decibels are derived from pressure, or power, as follows: Loudness in dBA = 20 x Log ( P / (2 x 10-5 ) ), or Loudness in dBA = 10 x Log ( E / 10-12 ). For example, say that P is the extremely quiet “threshold of hearing” of 0.00002 (or 2 x 10-5 ) pascals; this converts to 0 dBA, since Log ( (2 x 10-5 ) / (2 x 10-5 ) ) = Log (1) = 0. At the opposite extreme, if P is the painfully loud 200 (or 2 x 102 ) pascals, this equates to 140 dBA, since Log ( (2 x 102 ) / (2 x 10-5 ) ) = Log (107 ) = 7. The prime rationale for the decibel scale is that sound pressure levels exhibit a huge numerical “dynamic range.” The sound pressure level in the second example above (200 pascals) is 10 million times greater than the level in the first (0.00002 pascals). The logarithmic conversion to decibels makes these numbers more manageable (140 dBA and 0 dBA, respectively). Many familiar scales in science employ logarithms to handle large dynamic ranges. For example, the Sun appears 6.3 trillion times brighter than the dimmest star visible to the naked eye. The logarithmic star magnitude scale converts these brightnesses to manageable star magnitudes of –26 (for the Sun) and +6 (dimmest star). Similarly, in the logarithmic Richter scale used to measure the intensity of earthquakes, a Richter 3 is barely noticeable, while a Richter 8 quake, with 39 million times more energy, is devastating. Likewise, the Ph scale compresses wide variations in acidity to a 0-14 range. Logarithmic conversions change multiplicative ratios to additive differences. Here, multiplying the sound pressure level (in pascals) by 1.122 (which is 101/20 ) corresponds to adding 1 dBA to it; thus, adding 12% to a sound’s pressure level makes it 1 dBA louder. The same additive 1 dBA corresponds to multiplying the sound’s power level by 1.259, for an increase of 26% (note that 1.259 is 1.122 squared). Accordingly, an addition of 10 (or 20 or 30) dBA to a sound corresponds to a multiplication of the sound pressure level by a factor of 3.16 (or 10 or 31.6, respectively), or a multiplication of the power level by a factor of 10 (or 100 or 1000, respectively). These multiplications apply only to the raw physical pressure or power as it would be measured at a surface (e.g. an eardrum); they do not indicate differences in subjective loudness. In this subjective domain, it is generally agreed that a 10 (or 20 or 30) dBA addition corresponds to a perceived multiplication of loudness by a factor of 2 (or 4 or 8, respectively). |
DROWNING IN NOISE 17
The analytical core of this report is a procedure for estimating the noise increment — the increase above background noise levels — that a single jet ski causes for each beachgoer within range of its noise, and for translating the subjective annoyance caused by this excess noise into dollar terms. Later we generalize this into cost estimates for a “population” of beachgoers at one beach, and, ultimately, for the entire United States. Thus the analysis starts with two key questions about a “representative” beachgoer: how much louder do one or more jet skis render the beachgoer’s noise environment, and how do we represent the extra noise economically, in dollars of lost amenity?
These estimations unfold through a series of steps, each involving mathematical relationships specifying, for example, the rate at which noise diminishes with distance, or how a fluctuating noise compares in annoyance value with a constant noise. As well, a wide variety of “parameters” must be specified, e.g., what is the beach’s background noise level, without the jet ski, and how much annoyance occurs per unit of noise increment above that background?
Noise is a complex phenomenon, not least in its basic unit of loudness, the decibel (dBA), which is the logarithm of a physical quantity, acoustic power (see sidebar on previous page). Nor is it usual to see the impact of noise expressed in dollars. Accordingly, this section outlines and explains jet ski noise estimation and costing step by step. (Readers interested in a more detailed account of the technical nuances may refer to the Appendix.)
It will be helpful to keep the following points in mind:
Laws of Noise
DROWNING IN NOISE 18
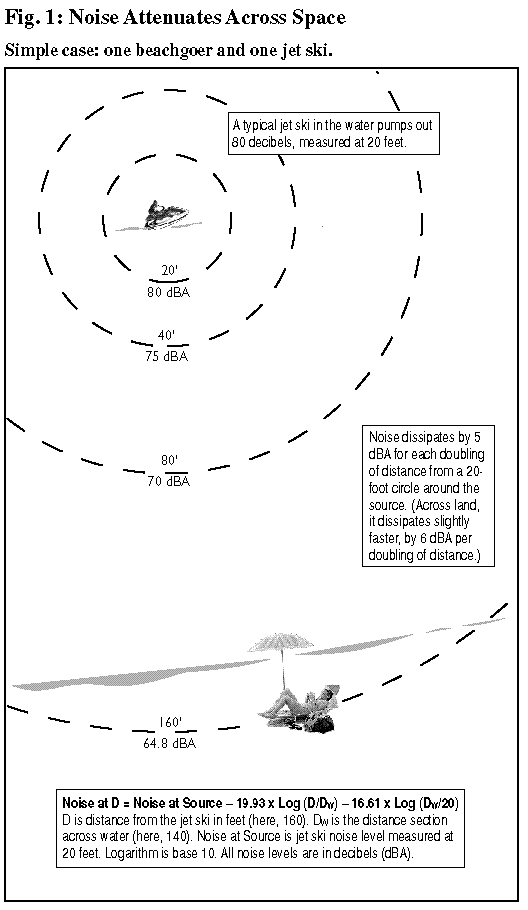
DROWNING IN NOISE 19

DROWNING IN NOISE 20
Key Noise Cost Precepts
DROWNING IN NOISE 21
|
Variable Noise is More Disturbing: Robinson’s Formula |
|
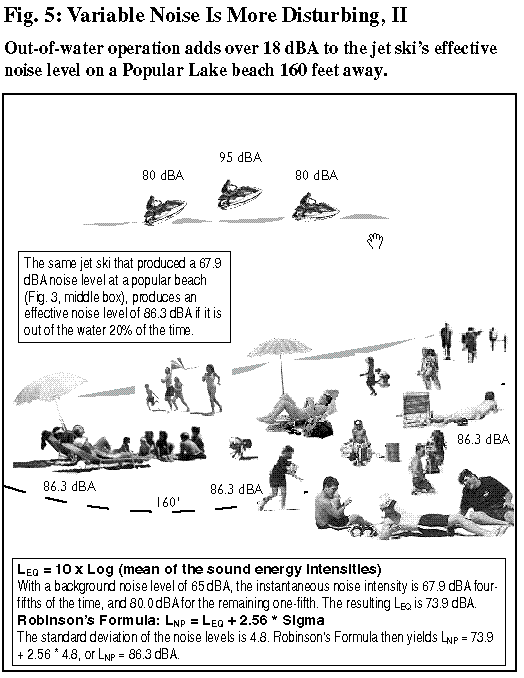
Researchers of humans’ perception of noise have long observed that varying noise is generally more disturbing than a steady noise — even when the steady noise is louder (contains more sound power) than the loudest of the varying noises. The reason, in a nutshell, is that varying noise demands the hearer’s continuous attention; it can’t be “tuned out.” In 1970, British acoustician Douglas Robinson gave a precise analysis of this phenomenon with the empirically derived relationship LNP = LEQ + 2.56 x Sigma. Here LNP is the Noise Pollution Level, or “effective” noise level — that is, the level at which a constant noise would be as annoying as the varying noise in question). LEQ is the mean noise power intensity converted to dBA; and Sigma is the standard deviation of the noise intensity in decibels. (All noise levels are as experienced by the beachgoer.) Through Robinson’s Formula, we can quantify the extent to which jet skis’ intermittent whirring and whomping noise profile is more annoying than other watercraft’s more constant sounds. This is no small matter, as the examples here of a jet ski operating 160 feet from a beachgoer on a secluded beach show. In Fig. 5, LEQ = 73.9 dBA (this is the mean noise power intensity, converted into dBA, when the instantaneous noise intensity is 67.9 dBA four-fifths of the time, and 80.0 dBA for the remaining one-fifth), and the standard deviation is 4.8 dBA. “Robinson’s Formula” then yields LNP = 73.9 + 2.56 x 4.8, or LNP = 86.3 dBA. In other words, a jet ski that continually leaves and then smacks against the water from 160 feet away will raise a 45 dBA background noise level to more than 86 dBA — a stunning 41 dBA impact. By comparison, in Fig. 3, the same jet ski would have raised the 45 dBA background noise level by just 20 dBA, to 64.9 dBA, if it had remained in the water the entire time. The difference in impacts is only partly due to the higher emission level when the jet ski is out of the water; the fluctuation in the noise level is as influential, if not more so. To a considerable extent, then, the power of jet skis to disturb is rooted in people’s sensitivity to varying noise signals. Jet ski manufacturers claim that their vehicles are no more disturbing than ordinary motorboats, but Robinson’s Formula, a fundamental result in psychoacoustics, clearly reveals the falsity of this claim. Perhaps even more importantly, it gives researchers the ability to quantify the actual noise impacts and costs. |
DROWNING IN NOISE 22
Input Assumptions
We now present the assumptions used throughout DROWNING IN NOISE to calculate the noise cost for a single beachgoer from a single jet ski. See the Appendix for derivation and justification for each.
· Jet ski distance from shore: between 50 and 10,000 feet, but heavily weighted toward the lower end (the additional distance from the water’s edge to the beachgoer is treated in Section 5). In the illustrations here, the distance between jet ski and beachgoer is assumed to be a constant 160 feet — much less than typical.
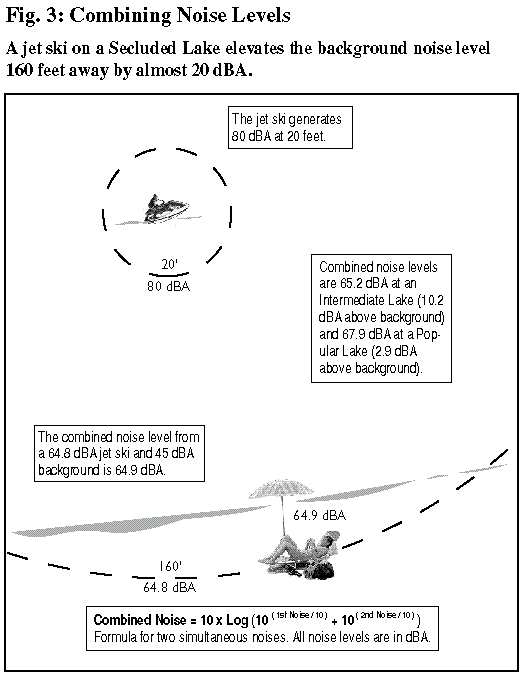
DROWNING IN NOISE 23
DROWNING IN NOISE 24
“Costing” the Excess Noise Imposed on Beachgoers
Value of a Beach Day
The accompanying illustrations depict jet skis raising beachgoers’ prior background noise levels. We now discuss how we translate these noise increments into dollars of negative value, or “disutility” in the parlance of economists.
The process begins with estimates of spending by the beachgoer to get to (and from) the beach, as well as other associated costs. These “actual expenditures” provide a lower-bound estimate of the economic value the beachgoer attaches to the day at the beach, since she must derive at least enough enjoyment to offset the cost of getting and being there (travel, parking, admission, extra food costs, etc.); otherwise, the visit wouldn’t be worth the expense of the trip.
In the Appendix, we discuss estimates of what beachgoers actually spend to access beaches in America, compiled by economists who study outdoor recreation. From these studies, we estimate that, as rough averages, visits to “popular” beaches, which by nature are easy to reach, cost beachgoers just $5 a day; visits to harder-to-reach
DROWNING IN NOISE 25
“secluded” beaches cost considerably more, $15 on average; visits to “intermediate” beaches entail spending the in-between figure of $10.
Consider a visit to an intermediate beach. The $10 expenditure represents only part of the value of the beach experience. Virtually all spending contains an element of value called consumer surplus, denoting the additional value to the buyer beyond the purchase price. I pay the $1.00 store price for a quart of milk, but I would have paid up to, say, $1.40; the 40¢ difference between the milk’s cost to me
DROWNING IN NOISE 26
and its value is my consumer surplus. Similarly, I may pay $299 to fly to London and back, but if I would have paid as much as $499, my consumer surplus for the fare is $200.
Economists have studied the consumer surplus associated with different kinds of expenditures. For discretionary purchases such as travel to a beach, consumer surplus is considered to be roughly equal in magnitude to the monetary expenditure.(9) That is, if a group of people paid an average of $10 each to get to an intermediate beach, the beach provided each of them with an average total value or enjoyment of about $20. Of this amount, one half offset the cost of the trip, and the other half corresponded to their consumer surplus, or net enjoyment over and above their direct outlay. The $20 total value of the beach experience is the sum of the actual expenditures and the consumer surplus.((10)
Value Loss from Adding Noise to a Beach
Next, we estimate the “degradation” of the beach experience due to the noise a jet ski imposes on the beachgoer. What we are seeking is a “Noise Depreciation Index” (NDI) capturing the extent to which a 1 dBA increment in noise level reduces the beachgoer’s enjoyment value of the day.
Beachgoers’ preference for quiet has never been quantified directly. Accordingly, our point of departure is people’s willingness to pay a premium to live in quiet as opposed to noisy neighborhoods, which has been extensively studied since the 1960s.
How similar are homeowners and beachgoers’ desire for quiet? Certainly, both groups want a noise-free environment; indeed, they are the same people, in different settings. Still, expectations and standards vary from one setting to the other; we believe that if anything, quiet is more central to beach enjoyment than to property values. Competing criteria such as safety, schools, transportation and neighborhood stability are important for housing values, whereas environmental and aesthetic considerations dominate in recreational settings.
This is not to say that beachgoers place quiet above all else; but for most, relief from the quotidian burden of intrusive noise — especially the ubiquitous noise of motors — is an important part of the expected and desired ambiance. Moreover, one can mitigate noise to
DROWNING IN NOISE 27

DROWNING IN NOISE 28
some degree on one’s own property by going indoors, shutting windows, or installing sound-insulating materials or muffling devices; a beach affords no such escape.
As we discuss in reviewing residential property studies in Part 5 of the Appendix, we believe that an NDI of 1% represents a reasonable estimate of the effect of noise on beachgoers’ enjoyment value of the day. It implies that to eliminate 10% of the enjoyment of a day at the beach, the noise increment due to the jet ski (or, equivalently, passing airplanes, dune buggies, etc.) must be 10 dBA.
That is an effect equivalent to replacing the noise level of a typical suburban area with that of a typical urban area or a busy office, as indicated in the table of noise levels on p. 14. Intuitively, it seems unlikely that an NDI of 1% overstates the degree to which each additional decibel reduces the beachgoer’s enjoyment value of the day.
Of course, people who attach greater value to quiet would tend to have a higher NDI, while others drawn to the beach primarily for “activity” would have a lower NDI. We believe an NDI of 1% is a reasonable mean encompassing a range of relative preferences between quiet and noise.
Jet Ski “Duty Cycle”
The discussion to this point assumes a jet ski hovering around the same area and operating nonstop all day. The first assumption is loosened in our model by treating the jet ski’s distance from shore as a “random variable,” as we discuss in Section 5. (Note that if the jet ski moved parallel to the beach, the same noise impact would simply be inflicted upon a different group of beachgoers, so the cost to all beachgoers would essentially be the same in our model. In fact, this understates the actual noise impact, because of noise-level variation as discussed in the sidebar on Robinson’s Formula, p. 21.)
The second assumption, pertaining to usage or “duty cycle,” requires us to qualify the model in Fig. 7. The issue is not that a jet skier may take an occasional break; since several users customarily take turns riding a single jet ski, most machines are in use nearly constantly. Rather, it is one of duration and timing of use.
Most beach and water use, by beachgoers and jet skiers alike, takes place over a six-hour period between the late morning, say 11 a.m.,
DROWNING IN NOISE 29

DROWNING IN NOISE 30
and the late afternoon, around 5 p.m. However, the average “beach- goer day” and “jet ski day” are both considerably shorter than six hours. We assume that a jet ski is driven for an average of three hours a day,(11) and that a beachgoer day similarly averages three hours long.
DROWNING IN NOISE 31
Thus, if the jet skier arrives at the beach early in the day and also leaves early, and if the beachgoers arrive and depart late, they miss each other, and there is no noise annoyance to the beachgoers. Conversely, if the jet skier and the beachgoer arrive (and depart) at the same time(s), then the “beachgoer day” is fully saturated with noise, and annoyance, from the jet ski.
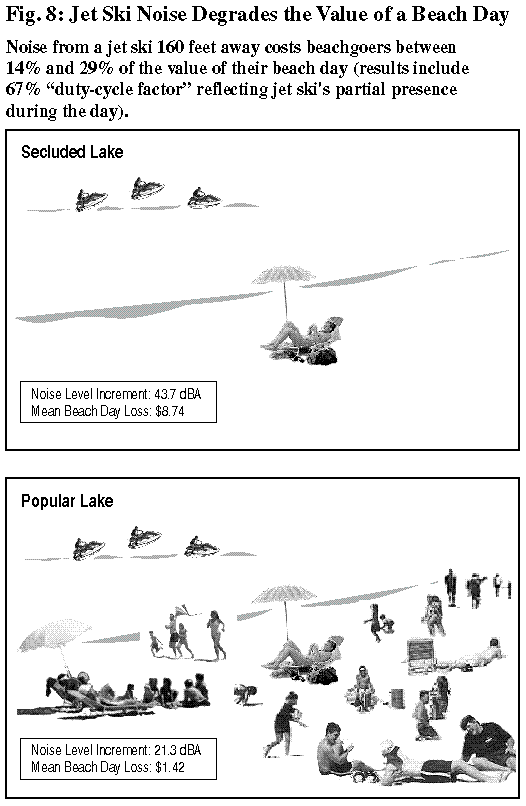
Perhaps surprisingly, the mathematical average (“expected value,” actually) of the overlap between the beachgoer and the jet ski is not one-half, but two-thirds. That is, if a jet skier and a beachgoer each spend three hours at the beach (both as contiguous three-hour blocks of time) over the course of a six-hour period of possible daily beach use (11 a.m. to 5 p.m.), the beachgoer will have the jet ski’s presence about two-thirds of the time.(12) Accordingly, two-thirds of the beachgoer’s beach-day value is affected. This requires that the calculation of lost amenity to this point, which assumes a full-day impact (with the value of a beachgoer day multiplied by the NDI and the excess decibel level), be multiplied by 0.67, as Fig. 8 illustrates.
Note that this simple two-thirds factor overlooks a psychological subtlety. Even after a jet ski has left the area, a beachgoer who has suffered through the noise annoyance has no assurance that the machine won’t return. Indeed, if she expects the cessation to be only temporary, then an anticipatory disturbance will likely persist through her remaining time at the beach. Accordingly, the two-thirds duty-cycle factor appears likely to understate jet ski noise costs for many beachgoers.
Factoring in the “duty-cycle factor” of 0.67, a jet ski at a 160-foot distance from a beachgoer typically imposes amenity losses ranging from a little under $1.50 per person at a popular beach, to almost $9 at a secluded lake beach, as Fig. 8 shows. In the “average” case reflected in Table 1 (p. 2), the per-beachgoer noise cost from one jet ski ranges from around 40 cents at a popular ocean beach to $7 at a secluded lake beach.
DROWNING IN NOISE 32
Introduction. In the previous section we outlined a model for estimating jet ski noise annoyance to one beachgoer on a specific beach, when a jet ski is a constant distance from shore. Here we describe an aggregate model for estimating noise costs for all of the beachgoers on six different classes of “beach types,” such as a “secluded lake” or “popular ocean,” with the jet ski distance from shore varying substantially. We believe the results are realistic estimates of the noise annoyance costs that jet skis impose on a beach full of people.
These estimates function as building blocks to estimate the aggregate disamenity of jet ski noise for the entire United States, in Section 6. They also may be used to assess proposals to control or eliminate jet ski noise in different beach environments, as we do in Section 8.
As noted earlier, we characterize beach types as either lake (bays, rivers and canals are subsumed under lakes) or ocean; and each beach is popular, intermediate or secluded, based on population density.
The beach (shoreline) lengths are assumed to range between 80 and 800 feet for lakes; the more expansive ocean beaches are assumed to vary in length between 200 and 2000 feet. Similarly, beach minimum and maximum depths (distance from water’s edge to the rear of the beach) are 20 and 80 feet, respectively, for lakes; and 50 and 200 feet, respectively, for oceans. (Dimensions are tabulated in Table 3 below.)
To calculate beachgoers’ noise increment from the jet ski, we must locate these beachgoers on the beach. We assume that the jet ski is evenly centered with respect to the beach, so that a perpendicular line drawn from the jet ski to the shore and extending to the back of the beach would divide the beach into two equal segments. We then distribute the beachgoers along the beach in equal left-to-right intervals, while letting their distance from shore vary randomly.(13) In effect, each beachgoer “commands” an area on the beach determined by the beach type and its associated population density.
For the jet ski we specify minimum and maximum distances from shore of 50 and 2,500 feet (roughly one-half mile), respectively, for lake-type beaches; and 50 and 10,000 feet (roughly two miles) for ocean beaches. The vast majority of jet ski operation appears to be within this range, both because most lakes, rivers, canals and bays are less than a mile across, and because jet skiers tend to operate close to
DROWNING IN NOISE 33
shore in any event. To reflect these phenomena, we locate the jet ski at a distance from shore given by a probability density that recognizes that jet skis tend to operate close to shore rather than very far away (see Appendix, Part 2).
Even so, our model produces an average jet ski distance from shore of 530 feet for lake (and bay and river) beaches, and an average distance of 1,365 feet for ocean beaches. Note also that the model assumes, for the sake of conservatism and simplicity, that at any particular (simulated) beach, the jet ski remains a constant distance from the shore. In fact, of course, the jet ski actually moves toward and away from shore over a rather wide range, causing additional noise level variation, and hence, additional disamenity that is not included in our model.
Now we need to account for jet ski “clustering.” Many jet skis are driven in pairs or in larger groupings. We assume that the average jet ski is part of a cluster of 1.6 jet skis (a statistical artifact akin to the proverbial “2.1-child-family”). This has the effect of adding just over two decibels (2.04 dBA, to be exact) to the 80 dBA mean emission level we have assigned to a single jet ski.(14)
To perform the actual calculations of excess decibels and disamenity costs for each beach, we adopt what mathematicians call a “Monte Carlo” approach (named for Monaco’s casinos, not for its beaches!). For each of the six beach types, we “computer-simulate” many (10,000) beaches of that type, each characterized by random values fitting the parameters defining that type.
Thus, to estimate the noise costs from a jet ski at, say, an intermediate lake, the computer constructs 10,000 such lakes — each with a population density of one beachgoer per 1000 square feet, with beach length varying from 80 to 800 feet and beach depth varying between 20 and 80 feet, as noted above. For each lake, the computer randomly spreads people along the beach and also assigns a jet ski to a distance between 50 and 2,500 feet from shore (between 50 and 10,000 feet for ocean beaches).
Each beachgoer’s noise-disamenity cost is then calculated from the excess decibels she experiences and the value she assigns to a beach day; and the sum of these costs for the different beachgoers becomes the jet ski noise cost for that one “trial.” That cost is then averaged with the costs calculated in the other 9,999 trials, giving the
DROWNING IN NOISE 34
results for the intermediate beach in the table on this page. (See Appendix, Part 2, for details.)
Jet Ski Noise Costs at Typical Beaches. Table 3 presents our estimates of the noise costs imposed on beachgoers at one beach by a jet ski cluster of 1.6 jet skis over the course of a day. The beach “input assumptions” are displayed in regular type, while the rows in boldface show the jet ski noise results — the additional noise experienced by the average beachgoer, the disamenity cost per beachgoer, and the disamenity summed across all beachgoers. The three bottom rows represent mean disamenity values for beaches of that beach type, computed over many beaches of that type.
The table shows that the added noise from a typical jet ski cluster is highest at the quietest beaches, with an average increment over back-
Table 3: Jet Ski Noise Costs per Beach per Day, by Beach Type
| Beach Type | Secluded Lake | Intermediate Lake | Popular Lake | Secluded Ocean | Intermediate Ocean | Popular Ocean |
| Min. length, ft | 80 | 80 | 80 | 200 | 200 | 200 |
| Max. length, ft | 800 | 800 | 800 | 2000 | 2000 | 2000 |
| Min. depth, ft | 20 | 20 | 20 | 50 | 50 | 50 |
| Max. depth, ft | 80 | 80 | 80 | 200 | 200 | 200 |
| Ft2/person | 10,000 | 1,000 | 100 | 10,000 | 1,000 | 100 |
| Population | 2.2 | 22 | 220 | 13.6 | 137 | 1376 |
| Bkground, dBA | 45 | 55 | 65 | 65 | 65 | 65 |
| Add. Noise, dBA | 37.0 | 26.0 | 13.7 | 7.6 | 7.6 | 7.6 |
| Utility/person | $30 | $20 | $10 | $30 | $20 | $10 |
| Cost/cluster | $16 | $76 | $201 | $21 | $139 | $697 |
| Cost/jet ski | $10 | $48 | $126 | $13 | $87 | $435 |
| Cost/person | $7.40 | $3.50 | $0.90 | $1.50 | $1.00 | $0.50 |
“Lake” subsumes bays, rivers and canals as well as lakes. Jet ski clusters average 1.6 jet skis each and are assumed to generate 82.04 dBA in water (80% of time) and 97.04 dBA out of water (20% of time), and to be randomly distributed between 50 and 2,500 feet offshore for lakes, and between 50 and 10,000 feet for oceans, but with closer distances predominating in all cases. Population is mean for each beach type. Utility/person is beachgoers’ mean value of day at the beach, without jet ski noise. Cost/cluster is total noise cost for entire beach, per day. Cost/jet ski equals cost/cluster divided by 1.6, and is not the same as the cost from one jet ski shown in Table 1. Cost/person equals Cost/cluster divided by Population (before rounding). Costs incorporate 0.67 duty-cycle factor.
DROWNING IN NOISE 35
ground of 37 dBA at the secluded lake beach and 26 dBA at the intermediate lake beach. The noise increment is lowest at the other beaches (popular lake and all oceans), for which the background noise level is assumed to be a uniform 65 dBA. (The average noise increment is higher (13.7 dBA) for the popular lake than for the ocean beaches (7.6 dBA), because more beachgoers are closer to the jet ski at the smaller lake beach.)
Noise costs per person are highest at the respective secluded beaches, and lowest at the crowded beaches, for two reasons: first, beachgoers at secluded beaches are assumed to place a higher value on their beach day; second, jet skis are more audible at quieter lake beaches. However, the noise cost per jet ski cluster (which is the summation of the per-person noise costs, across all beachgoers) is greatest by far at the popular beaches, as the increase in the population of beachgoers more than offsets the decline in per-person disturbance.
In addition, ocean beaches have higher noise costs than the corresponding lakes. This is because ocean beaches are larger, and thus present more people exposed to the noise.
The costs in Table 3 are averages for typical beaches and typical beachgoers. Actual beaches may be bigger or smaller than the figures shown here. For example, ocean beaches, as we define them, can reach as large as 2,000 feet long by 200 feet deep. A popular beach with those dimensions supports a population of 4,000 beachgoers, or almost triple the population mean shown in the table. The average beachgoer there would experience only a modest noise disamenity from jet skis, just 44¢ on average, but this would aggregate to $1,760 a day when summed over the huge beach population.(15)
At the other end of the scale is the secluded lake beach. By our definitions, lake beaches vary from as small as 1,600 square feet (80 feet long x 20 feet deep) to as large as 64,000 (800 x 80), and average around 22,000 square feet, or around half an acre. Since secluded beaches, by definition, have a population density of just 1/10,000 person per square feet, the average secluded lake beach has only 2.2 people — and is secluded indeed. But both of them would be intensely disturbed by jet skis, with a mean per-person disamenity cost of $7.40, or almost 25% of each beachgoer’s normal beach-day utility of $30. The total noise cost at this beach would be relatively small, however, at $16, because few people would experience the noise.
DROWNING IN NOISE 36
Annual National Jet Ski Noise Costs to Beachgoers. In the previous section we presented estimates of per-day jet ski noise costs to beachgoers for six “beach types”: popular, intermediate and secluded lakes (where the lake category also encompasses bays, canals and rivers), and popular, intermediate and secluded oceans. We now apply those figures to estimate an annual cost of jet ski noise to beachgoers for the entire United States of $908 million.
Calculating the national jet ski noise costs to beachgoers is straightforward, once we specify several assumptions about jet ski usage:
Number and usage of jet skis in the U.S. — We estimate that during 2000, the “base year” for this report, there are 1.3 million operable jet skis in America, and we assume that they are operated an average of 15 days a year. Both numbers are based on industry sources.(16) Combining the two assumptions yields 19.5 million “jet ski-days” of use per year in the United States.
Jet ski “clustering” — As noted in the preceding chapter, we assume that the average jet ski is part of a cluster of 1.6 jet skis. Accordingly, 19.5 million “jet ski-days” actually impinge on beachgoers as much fewer, 12.2 million, “jet ski-cluster-days” ( = 19.5 million / 1.6 ). Each jet ski cluster is louder than a lone jet ski by 2.04 dBA.
Jet ski distribution between lakes and oceans — The most comprehensive survey of jet ski owners to date, conducted for the jet ski industry in 1995, found that 71% of jet ski riding time is spent on lakes, 19% on rivers, 2% on canals, and 8% on oceans.(17) (Bays were not included as a category.) Rivers and canals (as well as bays) resemble lakes in both beach topography and wave height (which influences the background noise level). Accordingly, we place beach environments into two categories, lakes and oceans, and assign 92% of jet ski use to “lakes” (including rivers, canals and bays), and the remaining 8% to oceans.
DROWNING IN NOISE 37
Jet ski distribution among popular, intermediate and secluded beaches — We assume that 60% of jet skis are used around secluded beaches. While a majority of beachgoers congregate at popular beaches, the majority of beaches in America are secluded. (If 60% is too high, then we have understated the national noise cost, since each jet ski has a smaller total noise impact at a low-population beach than at a high-use beach.) We assign the remaining 40% of jet ski use equally (20% each) to intermediate-use and popular beaches. We also assume that the 20%/20%/60% jet ski distribution among popular, intermediate, and secluded beaches applies to both ocean and lake beaches.
From these assumptions, the 12.2 million jet ski clusters each year in the U.S. divide into roughly 6,700,000 at secluded lakes, 200,000 each at intermediate and popular oceans, and varying amounts at the three other types of beaches. Table 4 displays these usage figures and combines them with estimated per-usage costs for each beach type from Table 3, to yield the estimated total annual noise cost of jet skis to beachgoers in the United States.
As Table 4 shows, the estimated annual cost of jet ski noise to beachgoers in the United States is $908 million. An estimated $732 million of costs, 81%, are experienced at lakes, which we assume account for 92% of beaches frequented by jet skis. Popular beaches of either type (lake and ocean) comprise only 20% of beaches but almost 90% of beachgoers. Not surprisingly, they account for $587 million, or 65%, of the national jet ski noise cost to beachgoers.
Table 4: Annual Jet Ski Noise Costs to U.S. Beachgoers
| Secluded Lake | Intermediate Lake | Popular Lake | Secluded Ocean | Intermediate Ocean | Popular Ocean | |
| Jet Ski Distribution | 55.2% | 18.4% | 18.4% | 4.8% | 1.6% | 1.6% |
| Clusters / yr, millions | 6.7 | 2.2 | 2.2 | 0.6 | 0.2 | 0.2 |
| Noise Cost / Cluster | $16 | $76 | $200 | $21 | $140 | $700 |
| Annual Cost, millions | $110 | $171 | $451 | $12 | $27 | $136 |
| Annual Cost by Beach Type | All Lake Beaches: $732 Million | All Ocean Beaches: $175 Million | ||||
| Total Annual Cost | $908 Million | |||||
DROWNING IN NOISE 38
Noise costs per cluster are per day and are rounded from values in Table 3. Notes from that table apply here. Clusters per year are rounded; for exact values, multiply respective percentages in first row by 12,187,500.
Although secluded beaches are used by just 3% of beachgoers, they account for a substantial $122 million of annual noise costs, which is 13% of the national total. In particular, beachgoers at secluded lakes experience $110 million annually in lost amenity due to jet ski noise. While by definition each secluded lake has few beachgoers, jet ski usage there imposes high noise costs due to the large number of such sites, the high value that visitors to secluded areas place on their recreation day, and the low background noise that makes jet skis particularly audible.
The $908 million total cost per year equates to an average of $698 per year in noise costs to beachgoers per jet ski in the United States, and to $47 per jet ski per day of usage, where a “day” is defined as three hours of usage. That is, in the course of a day’s use the typical jet ski operating in America imposes $47 worth of noise pollution costs on beachgoers. To be sure, jet skis that avoid popular beaches, or remain far from shore and are operated conservatively, or congregate in clusters with other jet skis, impose lower costs. Conversely, jet skis that hover near popular beaches or are particularly loud emitters or operate solo create even more total disamenity.
DROWNING IN NOISE 39
The dollar amounts in Table 4 in the previous section purport to represent what Americans would be willing to pay to rid their beaches of jet ski noise — if there were an agency that would take their money and turn off the noise. Are these results plausible?
We believe so. To be sure, $908 million a year may seem high for damage that is primarily aesthetic.(18) But this figure has been derived meticulously and appears commensurate with the nationwide level of jet ski usage, as well as the frequency of beachgoing and the importance Americans attach to it.
At the same time, we recognize that this national noise-cost figure is built on many assumptions — the sidebar on p. 40 shows 17, of which 7 pertain to an individual jet ski, 2 describe an individual beachgoer, another 4 concern the beach type, and 4 generalize from a single beach to the entire country. While some of these parameters are known to a high degree of precision — e.g., number of jet skis in the U.S., or rate of noise dissipation — others had to be approximated and may only be accurate to a factor of two. Verifying and fine-tuning these parameters is an area for future research.
It is a truism in research that as analysis ventures further from known terrain, the results become less accurate. Each step necessarily introduces new uncertainties. Clearly, our estimates of jet ski noise annoyance are more accurate at the “excess dBA” level of description than at the “dollars” level, since the latter requires two additional assumptions — the dollar value of a beach day to a person (#8 in the list) and its rate of devaluation per excess dBA from jet ski noise (#9). Likewise, the results for a particular beach, for which size, population density, and background noise level are known or can be easily measured, will be more accurate than the results for one of our six beach types, whose parameters are only known statistically.
Least precise, then, are our national results, relying, as they do, on national beach use data and assumptions. This is to be expected. Several years ago, researchers at the University of California of Davis published an entire volume dedicated to calculating the annual cost of all U.S. motor-vehicle noise. They concluded that the cost lay between $140 million and $56 billion — a 400-fold range.(19)
DROWNING IN NOISE 40
|
Parameters for Estimating
|
| Individual Jet Ski Parameters 1.
Jet ski distance
2. Jet ski loudness in water 3. Jet ski loudness out of water 4. Jet ski % of time in/out of water 5. Jet ski duty cycle 6. Jet ski “clustering” 7. Rate of noise dissipation (across water and across land) Individual Beachgoer Parameters 8. Beachgoer mean beach-day value 9. NDI (Noise Depreciation Index) Beach Parameters 10. Beach length 11. Beach depth 12. Beachgoer population density 13. Beach background noise level National Jet Ski Usage Parameters 14. Number of jet skis in America 15. Jet ski days per year 16. Distribution of jet skis among beaches: secluded / intermediate / popular 17. Distribution of jet skis among beach types: lake / ocean |
Of course, the UC Davis analysis encompassed many classes of vehicles, and it considered the full spectrum of noise costs. Still, it suggests that in estimating national noise costs from jet skis, alternative (but still reasonable) assumptions might produce results differing from ours by a factor of two or three. Note, however, that alternate estimates are likely to exceed, rather than undercut, ours, due to the intentional conservatism of our input values.
On the other hand, a very high degree of confidence can be attached to our mitigation analyses, which appear in the next section. These “relative” results estimate the degree to which changes in jet ski usage or noise generation would reduce the overall noise annoyance. They are bound to be more accurate — “robust” in the parlance of policy analysis — than “absolute” results such as noise costs for the entire U.S. or even for a single beach, since any mis-specifications in our assumptions will likely be mutually canceling.
DROWNING IN NOISE 41
In this section, we discuss how the noise costs of jet skis to beachgoers might be reduced. We do this by varying several “input parameter” values in the national noise cost model, and observing how the estimated noise cost changes as a result. This sensitivity analysis enables us to gauge the effectiveness of mitigation strategies such as restrictions on usage or engineering changes to new jet skis. Similarly, we can estimate how much, say, jet ski distances from beaches must be increased, to reduce overall jet ski noise costs significantly.
The reader should bear in mind that some steps in the noise cost calculation involve “non-linear” mathematical relationships, as well as random variables. As a result, mitigation strategies generally cannot be assessed by applying simple ratios. For example, the fact that the average noise increment from a jet ski cluster on a popular ocean beach is 7.6 dBA, does not imply that the jet skis would be inaudible if they were made 7.6 dBA quieter. In fact, an average reduction by that amount would eliminate just 63% of the aggregate beachgoer noise impact rather than 100%. Similarly, the reduction in noise from doubling the jet skis’ minimum distance, or even average distance, from shore, cannot be predicted a priori, but must be calculated through the noise cost model.
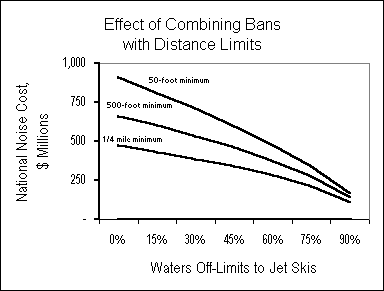
Here we apply sensitivity analysis to vary three jet ski characteristics: minimum distance from shore, engine noise level, and the number of waterways made off-limits to jet skis. For each, we have determined the changes in these characteristics that would be necessary to reduce by 25%, 50% and 75% today’s $908 million national jet ski noise cost estimated in Section 6. The results are presented in Table 6, for two cases: a “2000” case based on the current (1.3 million) number of jet skis operating in the U.S.; and a “2005” case pegged to the 1.8 million jet skis projected to be operating five years from now.
As Table 6 indicates, to eliminate three-fourths of the nationwide noise cost of jet skis today, either all existing jet skis would need to be made vastly (14 dBA) quieter, or jet skis would have to be barred from 85% of all waterways. For the same result of a 75% reduction in noise costs, but incorporating anticipated growth in usage in 2005, either all jet skis — again, existing as well as new models — would need to be made 16 dBA quieter, or jet skis would have to be barred
DROWNING IN NOISE 42
Table 6: Jet Ski Use/Design Changes to Reduce Noise Costs
| Base Case | 25% Drop in Costs | 50% Drop in Costs | 75% Drop in Costs | ||||
| Mitigation Strategy | 2000 | 2005 | 2000 | 2005 | 2000 | 2005 | |
| Minimum Distance (ft) | 50 | 450 | 1170 | 1600 | NA | NA | NA |
| Noise Reduction (dBA) | 80 | 3 | 7 | 8 | 11 | 14 | 16 |
| % of Waters Off-Limits | 0% | 34% | 58% | 63% | 76% | 85% | 90% |
Base column shows mean values assumed in this report. Other columns show parameter values required for all jet skis, to reduce year-2000 national noise costs by 25%, 50% or 75%. “2000” values assume changes are made “overnight”; “2005” values assume changes are made for the expanded fleet of jet skis in that year. “NA” denotes that the indicated goal cannot be achieved through that strategy. Changes in jet ski characteristics are made one at a time. Combined strategies are shown in Table 7 on p. 48.
from 90% of all waterways. Needless to say, the technical (not to mention political) impossibility of retrofitting the existing 1.3 million jet skis in the United States renders the option of even a moderately quieter jet ski fleet completely infeasible.
The more modest goal of eliminating one-fourth of jet ski noise costs could be reached today either by placing 34% of all waterways off limits, or keeping jet skis at least 450 feet from all shorelines (except to dock, and then only very slowly). Table 6 also shows the stronger measures required to maintain a 25% noise cost reduction in 2005 in the face of growth in the number of jet skis. Either the share of waterways from which jet skis are barred would have to be raised significantly, to 58%, or the distance limit would have to be extended to 1170 feet, between a fifth and a quarter of a mile.
We now discuss these results in detail.
Increase jet ski distance from shore. As noted in Section 5, we assume that jet skis’ distances from shore vary over a wide range, from as little as 50 feet from shore to as much as 2,500 feet for lakes and 10,000 feet for ocean beaches (approximately half a mile and two miles, respectively). In recognition of the common preference of jet skiers to operate relatively close to shore, we constructed our model to assign progressively higher probabilities to smaller distances. The result is that for lake beaches (encompassing lakes, bays, rivers and canals), the average jet ski distance in our model is 530 feet — one-tenth of a mile, or two or three small city blocks; while for ocean beaches
DROWNING IN NOISE 43
the average jet ski distance from shore is 1,365 feet, or just over a quarter-mile.
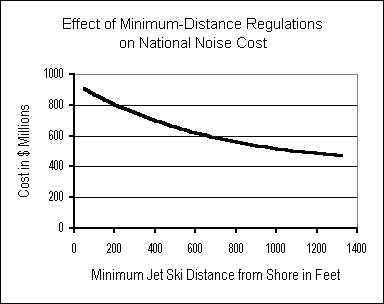
Requiring jet skis to operate far from
shore reduces noise costs
to beachgoers only modestly, because sound carries well across
water.
A 500-foot limit reduces costs by just 27%, on average.
A number of jurisdictions prohibit jet skis from operating closer to any shoreline than 500 feet (with exceptions for launch access, for which jet skis must be driven slowly, hence less noisily). At best, such ordinances will reduce noise levels to beachgoers only modestly. Sound simply carries too well across water for 500-foot minimum-distance limits to be truly effective.
We estimate that even with perfect compliance — which is by no means assured — a 500-foot rule would reduce noise costs to beachgoers at an average beach by only 27%. Allowing for anticipated growth in usage, if a 500-foot rule was applied universally but as the only mitigation strategy, the national jet ski noise cost in 2005 would be no smaller than today (in fact, we estimate that it would be 1% higher).
DROWNING IN NOISE 44
|
When a Distance Limit Becomes a Ban |
||||||||||||
|
On sufficiently small lakes, rules prohibiting jet skis from operating close to shore can function as outright bans, as operators literally run out of room to drive their vehicles. We estimate that a 500-foot rule effectively bars jet skis from lakes under 85 acres — smaller if the lake is unusually round; larger if it is unusually elongated or irregular. Similarly, where a quarter-mile rule is in effect, a lake must be around 340 acres or larger — slightly over half a square mile — to support a jet ski, as the table shows.
(We assume ellipse-shaped lakes twice as long as wide, and a 20-acre zone at the center for maneuvering.) Accordingly, on ponds and small lakes, distance limits may act as bans. Our model examines distance limits and outright bans separately and thus does not reflect this convergence. |
Part of the drawback of a 500-foot rule is that it pushes the average jet ski only 300 feet further out, on average, and therefore attenuates the noise impact on beachgoers only modestly. A more stringent quarter-mile minimum-distance rule, which San Francisco among other municipalities has enacted, has almost twice the noise-reducing effect of a 500-foot rule, reducing beachgoer noise costs by 48% at an average beach. Of course, growth in usage would diminish the effectiveness of this strategy as well; we estimate that under a universal quarter-mile rule, national noise costs in 2005 would be just 28% less than today’s figure, because of an 38% rise in the number of jet skis.
Reduce engine noise. As shown in the middle row of Table 6, national jet ski noise costs would be cut by 22% if it were possible to make an immediate 3 dBA reduction in engine noise emissions from all jet skis — that is, to reduce our estimated average of 80 dBA to 77 dBA (with the jet ski noise level measured “in the water” at 20 feet).
DROWNING IN NOISE 45
Further cuts would require steeper drops in noise output. In order to make a significant difference — on the order of 75% — the average base noise level of all jet skis in use would need to be reduced immediately from 80 dBA to 66 dBA. (A 14 dBA drop such as this is equivalent to eliminating 96% of a large number of identical, simultaneous noise sources.) Further reductions of 2-3 dBA would be required to stabilize national noise costs at this sharply reduced level in the face of growth in usage to 2005.
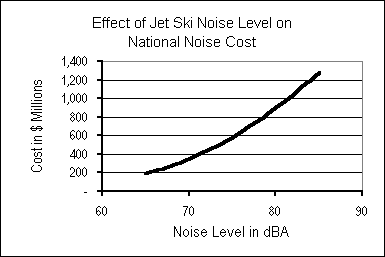
Noise costs are sensitive to jet ski
noise level (as measured here from 20 feet,
with jet ski in the water). The evidence is weak at best that new
models
are quieter than the 80 dBA mean assumed in this report.
Unfortunately, these figures are completely hypothetical, since there is no possibility that the existing “fleet” of 1.3 million jet skis will be retooled to reduce noise emissions. Any changes to engine designs would affect new models only, which are being sold at a rate of 150,000 a year. At an estimated retirement rate of 50,000 machines per year, it will be half-a-dozen years before the number of present-day machines, with their average 80 dBA noise level, drops below one million.
Of course, new models do present some opportunity to develop and deploy quieter jet skis. Several jet ski manufacturers as well as the industry trade association now tout a number of measures, ranging
DROWNING IN NOISE 46
from adding or expanding mufflers, baffles and insulation to redesigning intake and exhaust systems. These design changes, they assert, make new jet skis 50-70 percent quieter than their predecessors,(20) a range of improvements that would nominally correspond to drops in noise levels of up to 8 dBA.
However, the lone new jet ski model for which data were available appears to have a noise level of 83 dBA, or 3 dBA louder than our estimated 80 dBA average for all jet skis now in use.(21) Indeed, with market share rising for higher-horsepower jet skis designed to carry two, three or even four persons, new models may well be no quieter, on average, than our assumed 80 dBA mean for the current fleet.
The most optimistic scenario, then, is that all new jet skis (those put in service in or after 2001) would have in-water emission levels of 75 dBA rather than the 80 dBA average assumed for machines to date. But even with this generous assumption, the national noise costs of jet skis in 2005 would grow to approximately $1.075 billion, a level 18% greater than today’s cost, due to the projected 38% increase in the number of machines in use. Even under a hypothetical “crash” program that doubled the noise suppression gains from new models (to 10 dBA) and also doubled the rate at which they replace noisier older models, jet skis’ nationwide noise costs in 2005 would still be within 8% of year-2000 costs, at $832 million.
This is not to say that engine noise reductions have no value. On average, the noise increment to a typical beachgoer from a 75 dBA jet ski is 35% less than that of an 80 dBA machine. “Source noise” emission reductions of at least 5 dBA should be required for all new jet skis, with further improvements aggressively timed to meet or even force new product development cycles. But such measures should be regarded as only an adjunct to approaches that restrict jet ski use.
Concentrating usage at fewer waterways. The most effective noise-reduction strategy is banning jet skis from a large percentage of lakes, bays, rivers, canals and oceans.
According to our model, bans would have less-than-proportional effects on noise costs. For example, an 80% ban (i.e., covering 80% of lakes, bays, etc.) would reduce overall noise costs by 69% rather than 80%. This is because, by our assumptions, the entire jet ski fleet would “migrate” to the remaining 20% of waters. The assumed five-
DROWNING IN NOISE 47
fold increase in jet ski use on those lakes and other waters would raise noise costs there by 57%, on average.(22)
Still, widespread creation of jet ski-free beaches and waters is the only approach that is both technically feasible and could also have a significant impact on jet ski noise costs in a region or nationwide in the near term. As Table 6 shows, making 85% of U.S. beaches jet ski-free would eliminate three-quarters of national jet ski noise costs overnight, reducing the annual disamenity to beachgoers from $908 million a year to $229 million. Extending the ban to 90% of beaches would maintain this lower level of noise costs in the face of anticipated growth in usage to 2005.
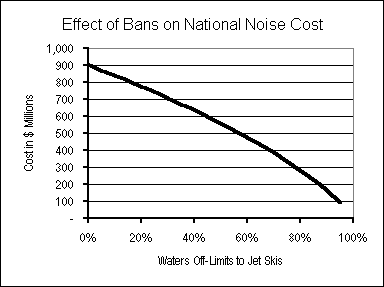
The only effective noise-cost reduction
strategy is banning
jet skis altogether. Making 90% of waters jet-ski-free would
eliminate 82% of the machines’ total noise impact — more if
usage
would drop as a result.
Outright bans have another advantage: they are simple to administer, whereas both minimum-distance regulations and noise emission limits would require constant (and expensive) monitoring and adjudication. Whether widespread bans can be enacted over the opposition of jet ski manufacturers and user groups is of course unclear,
DROWNING IN NOISE 48
but there is no question that banning jet skis from a large majority of U.S. waters would reduce jet ski noise costs significantly.
Combined mitigation strategies. Because the three mitigation strategies approach jet ski noise reduction in different ways, any two of them, or all three, may be combined, as we do in Table 7 on the next page.
Table 7: Bans Required to Meet Noise Cost Reduction Goals
| Date | Minimum Distance | Quieter New Jet Skis? | Reduce by 25% | Reduce by 50% | Reduce by 75% |
| 2000 | 500 feet | Not applicable | 0% | 46% | 80% |
| 2000 | ¼ mile | Not applicable | 0% | 7% | 71% |
| 2005 | 500 feet | Yes | 21% | 58% | 84% |
| 2005 | ¼ mile | Yes | 0% | 31% | 78% |
| 2005 | 500 feet | No | 39% | 67% | 87% |
| 2005 | ¼ mile | No | 0% | 48% | 82% |
Cell entries in last three columns show percent of lakes, bays, etc. from which jet skis would need to be banned to achieve respective reductions in national noise costs. Bans would operate in conjunction with one of two distance rules shown; and, in middle two rows, with 5 dBA noise reductions in all jet skis sold after 2000. Entry of 0% denotes goal can be reached without bans.
Comparing Table 7 with Table 6 (p. 42), which presented mitigation strategies singly rather than in combination, we see that minimum-distance rules and noise reductions for new jet skis could allow noise cost reduction goals to be met with somewhat less-sweeping jet ski bans; still, bans would need to be widespread to reduce national noise costs significantly (by 75%).
To reduce noise costs by 25%: A universal 500-foot rule would cut noise costs to beachgoers by 25% “overnight,” assuming perfect compliance. Sustaining that reduced level to 2005 would require either extending the minimum distance to a quarter-mile, or, if the 500-foot rule were maintained, banning jet skis from 39% of all waters. (If all new jet skis are 5 dBA quieter, the ban could be scaled back to 21% of lakes and other waters.)
To reduce noise costs by 50%: If we consider the upper limit of feasible minimum-distance rules to be a quarter-mile, then distance rules alone cannot halve national jet ski noise costs to beachgoers, as Tables 6 and 7 show. For an overnight 50% reduction, either jet skis
DROWNING IN NOISE 49
must be eliminated from 7% of waters and barred from approaching within a quarter-mile of all shorelines elsewhere; or they must be banned from 46% of lakes, rivers, etc. and barred from operating within 500 feet of all other shores. To maintain that level of cost while usage grows during the next five years, jet skis would have to be banned from between one-third and two-thirds of all U.S. waters (with the fraction depending on which minimum distance was applied, and whether new machines were quieter).
To reduce noise costs by 75%: Table 7 shows that achieving a 75% reduction in jet ski noise costs to beachgoers overnight would require a quarter-mile distance rule in conjunction with a 71% ban. For the same result but absent minimum-distance rules, jet skis would have to be banned from 85% of waters, as Table 6 shows. Accordingly, the “choice” for a 75% noise cost reduction today is between permitting jet skis at roughly 30% of waters and keeping them at least a quarter-mile offshore at the other 70% of beaches; or allowing jet skis to operate unrestricted but at just 15% of waters.
Similarly, for 2005, under the optimistic assumption that all new jet skis sold are 5 dBA quieter, the choice is between allowing jet skis at 22% of waters while barring operation within a quarter-mile of shorelines at the other 78% of beaches; or allowing unrestricted operation at just 10% of waters.
Of course, the most powerful approach is to use all three mitigation strategies vigorously, and in combination. We estimate that limiting jet ski use to 10% of U.S. waters, and restricting operation there to at least a quarter-mile from shore, would eliminate 88% of noise costs to beachgoers nationwide. Maintaining these restrictions while requiring all new jet skis to be 5 dBA quieter than the current average would yield an 85% reduction in national noise costs in 2005 compared to today’s level, despite a projected 38% growth in the number of machines in use.
“Beach type”-specific strategies: Each of the three approaches discussed here may be more or less effective in reducing noise costs at particular beach types (e.g., secluded ocean, popular lake, etc.). While analyses of “beach type”-specific strategies are beyond the scope of this report, it would be worthwhile to consider which strategies would deliver the greatest noise cost reductions at each of the six beach types defined in this report. (See Appendix, Part 8 for information
DROWNING IN NOISE 50
on using our jet ski noise cost model.) Similarly, jet ski noise at a particular site could be analyzed using the single-beach model described in Section 4.
“Time-sharing” beaches: Another mitigation approach is to restrict jet skis to certain hours of the day. For example, their use might be permitted during the “first half” of the nominal beach day (between 11 a.m. and 2 p.m.), and forbidden during the “second half” (2-5 p.m.) While this approach might appear to eliminate half of jet ski noise costs, the actual reduction would be considerably less — perhaps only 25% — and would depend on how both beachgoers and jet skiers modified their schedules as a result.(23) Still, “time sharing” (or, more accurately, temporal segregation) could be a useful supplemental strategy, and is deserving of further study.
Noise taxes: The noise costs of jet skis could be “internalized” by taxing their sale and/or use. Pollution taxes are attractive not only because they generate revenues that can be used for environmental remediation, but because they act as an economic disincentive to the activities that create the pollution. In the case of jet skis, a tax reflecting the costs of noise and, perhaps, other environmental harms from jet skis, such as their prolific generation of air pollutants, could fund additional policing and rescue operations as well as purchase of sensitive beach environments, while discouraging usage.
In Section 6, we calculated that the typical jet ski imposes roughly $47 in noise costs on beachgoers per day of usage, or an average of $700 each year. We estimate that taxes on jet skis at these levels would eliminate around half of jet ski use and, accordingly, of jet ski noise in the United States. That is, if users of jet skis were forced to pay either a $700 fee for a year’s usage (through an annual registration charge), or a daily use fee of $47, roughly half of current usage would cease as users found the cost prohibitive and substituted other forms of recreation. A milder tax, corresponding to half of the average jet ski’s noise costs ($350 a year or $23 a day), would reduce usage by an estimated one-third. (See Appendix, Part 6, for derivation of these results.)
Time jumping out of water: Sensitivity analysis makes clear the centrality of “jumping out of water” operation and rapid maneuvering to jet ski noise. We have calculated that if jet skis never left the water, so that engine noise remained muffled and the vexing “whomp
DROWNING IN NOISE 51
whomp” disappeared, and if the equally irritating rapid maneuvering and frequent speed changes were eliminated as well, the nationwide jet ski noise cost would be approximately 84% less than at present.
Two factors contribute to this result: first, engine noise is much less without the instantaneous 15 dBA increment associated with leaving the water; second, the moment-to-moment variability of the noise, which contributes greatly to its annoyance to listeners, is effectively eliminated. In any event, one can say that fully five-sixths of the noise impact of jet skis results from out-of-water use and rapid maneuvering.(24)
In theory, then, the national noise cost of jet skis could be cut significantly if jet skis never left the water or engaged in rapid speed changes. Unfortunately, there does not appear to be any feasible means of accomplishing this. As noted earlier, leaving the water is not just a matter of wake-jumping; it is a natural concomitant of the high speeds that are intrinsic to jet skiing, coupled with the vehicle’s short hull. Without universal speed limits, along with restrictions on deliberate jumping out of the water, the share of time that jet skis leave the water or practice rapid maneuvers is unlikely to diminish.
DROWNING IN NOISE 52
As we stated in the Executive Summary, the subject of this report — and of our Jet Ski Noise Cost Model through which we generated our findings — is jet ski noise and its cost to beachgoers. However, jet skis impose noise costs on property owners and water recreationists as well, and also cause non-noise pollution and injury damage. In this section we discuss these cost areas and offer rough estimates.
Residential property costs of jet ski noise. Jet ski noise resounds not only on beaches but at houses, resorts and other properties at or near beaches and shorelines. Although (presumably) the average noise increment from jet skis would tend to be less at these sites than at beaches, due to distance-related attenuation, the impact per house could be considerable where jet skis are a frequent presence. As well, the sheer number of beachfront houses in America guarantees that the total impact of jet ski noise at waterfront properties will be large.
Our noise cost model is well-suited to estimate residential impacts of jet ski noise for a particular property, for all properties along a beach, or for a region. Although that application was outside the scope of this report, we have made an exploratory calculation of the total national cost of jet ski noise at U.S. residential properties.
We estimate that:
DROWNING IN NOISE 53
These assumptions yield an annual residential property noise cost from jet skis of some $230 million, or 25% as much as the estimated noise impact on beachgoers.(26) This exercise, while only a sketch, suggests that jet skis impose considerable noise pollution costs on people in and around beachfront properties as well as at beaches.
Jet ski noise costs to other water users. In addition to beachgoers and beach homeowners or renters, boaters are affected by jet ski noise. The impacts are clearly most severe for users of human-powered craft — canoeists, kayakers and rowers — as well as for sailors and windsurfers and, of course, surfers and swimmers.
Although the danger to boaters and swimmers from hot-rodding jet skiers has been noted widely (see discussion on pp. 55-56), no price tag has been attached to the noise costs borne by these water users. Yet quiet — indeed, an aural environment free of motorized sound — is central to the experience of using both human- and wind-powered watercraft. Arguably, no one suffers jet ski noise more keenly than the paddler whose exploration of placid coves and inlets is shattered by the roar of jet skis.
Here too we venture a preliminary, suggestive calculation of national noise costs. We begin with the 12.2 million jet ski “clusters” posited in the national beachgoer analysis in Section 6. We assume that only one out of every two jet ski clusters disturbs any watercraft users; that each such cluster disturbs two people; that the added noise level from the jet ski cluster averages 37 dBA, the same as the added noise imposed by jet skis on beachgoers at a secluded lake;(27) that the utility or value of a day spent kayaking or canoeing is double the midpoint of the $10-$30 range for beachgoing, or $40.(28) We apply our standard NDI (Noise Depreciation Index) of 1.0%, although arguably quiet is even more highly prized by non-motorized boaters than by the average beachgoer.
These assumptions yield an annual national cost of jet ski noise to other water users of approximately $120 million, or 13% as much as the $908 million jet ski noise cost estimated for beachgoers.(29) While this exercise, like the residential cost discussion preceding it, is preliminary, it indicates that jet skis impose significant noise pollution costs on other recreational water users. Extending our model to encompass these costs would be a valuable step, as would analysis of
DROWNING IN NOISE 54
jet ski noise annoyance costs for hikers and walkers on trails, promenades, scenic overlooks, etc. near beaches and waterways.
Jet ski air pollution costs. Jet skis, like snowmobiles and other all-terrain vehicles (ATV’s), are prodigious emitters of carbon monoxide, particulate matter and smog-forming hydrocarbons. We estimate that per hour of use, the average jet ski pollutes the air at around 60 times the rate of an average automobile (see sidebar below; “auto” as used here is a composite average of cars and light trucks).
|
Air Emissions: Jet Skis vs. Automobiles |
|
In 1998, the California Air Resources Board published the startling finding that a jet ski operating for just two hours produced the same exhaust emissions as a 1998 passenger car operated for over 100,000 miles. This statistic has received wide circulation, but it should be tempered in two respects. First, CARB’s baseline 1998 car was a new model meeting strict California standards, making it roughly 5 times cleaner than the average automobile (car or light truck) in use in the U.S. Second, the comparison should be broadened from hydrocarbons, which jet skis emit in particular abundance, to the full mix of gasoline-engine pollutants. Even with these adjustments, jet ski emission rates per hour of use exceed those of autos 60-fold. Following is an outline of the calculations: Emissions Comparison (all figures in grams) Hydrocarbons + Nitrogen Oxides (NOx)
Carbon Monoxide (CO) Jet ski: 263/hp-hr x 80 hp x 0.5 engine load factor = 10,500
g/hr
Jet ski emission factors are from CARB, 1998. 80 horsepower is authors’ estimate for jet skis currently in use; figure is rising with higher-power newer models. Load factor is CARB assumption for load on engine, rather than duty cycle as used here. Car emission factors are authors’ interpolation for 1999 of year-1995 and year-2000 on-road averages for U.S. autos (Ross, 2000): 1.0, 1.5 and 15 g, respectively, for HC, NOx and CO in 1995; 0.7, 1.0 and 10 g for 2000. Hydrocarbon and NOx emissions are often combined in pollution evaluations, since both harm humans primarily by reacting, in sunlight, to produce photochemical smog. In averaging the respective ratios (90 for HC and NOx; 25 for CO) to yield 60, we rounded upward to reflect the greater health impacts of HC and NOx vis-a-vis CO. |
DROWNING IN NOISE 55
Considering that the family auto is still a big pollution source (despite notable reductions in per-mile pollution in recent decades), a single jet ski is an enormous polluter. Although use of jet skis is dwarfed by use of autos,(30) jet ski exhaust could be adding 10% to nationwide emissions from auto tailpipes, making it a genuine environmental problem.
Indeed, a first-cut estimation of jet ski air pollution costs to humans yields disturbing results. In a particularly rigorous analysis, McCubbin and Delucchi found that the average light-duty gasoline auto in use in America in 1990 created at least 0.6¢ of air pollution “health effects” costs per mile driven. (The upper end of their cost range was a dozen times higher.(31) )
Even if this figure is halved to reflect antipollution progress since 1990, and is further reduced by one-third to reflect that jet skis are typically operated further away from people than are cars, it suggests that in just an hour of use a typical jet ski generates enough air pollution to cause at least $4 worth of health costs; over the course of a three-hour “jet ski day,” the damage would be at least $12, in addition to the $47 average daily noise cost to beachgoers per jet ski. Extrapolating to the entire U.S., with an estimated 19.5 million “jet ski days,” yields at a minimum, a $240 million annual health bill for air pollution from jet skis.
If jet ski air pollution costs are indeed in that vicinity, let alone higher, stringent regulation should be a high priority. However, as a matter of engineering, sharp reductions in jet skis air emissions would appear to be a considerable challenge. Jet skis, like other ATV’s, use two-stroke engines. These dump considerable amounts of the fuel unburned into the water, sometimes 20% or more, and also are prone to burning lubricating oil which mixes with the gasoline.
Cleaner four-cycle engines aren’t well-suited for jet skis, because they have a lower power-to-weight ratio and are susceptible to flooding and stalling when water is ingested with the air supply. The likely persistence of high air emissions from jet skis strengthens the argument for pollution taxes on their sale and/or use in order to internalize their environmental costs and discourage usage — or at least spur development of cleaner models.
DROWNING IN NOISE 56
Jet ski physical injuries and ecosystem damage. Accident and injury rates for jet skis are starkly disproportionate to their share of recreational watercraft. According to U.S. Coast Guard data for 1997 (the most recent year for which data are available), more than half of all serious recreational boating collisions — accidents resulting in injuries requiring more than first aid, or property loss over $500 or loss of vessel — involved one or more jet skis.(32) Yet jet skis accounted for fewer than 10% of registered watercraft in that year, suggesting that jet skis’ participation rate in serious collisions, per hull, is a dozen times that of other boats.
To derive the corresponding figure per hour of use, one would need to know the rate of use per hull for jet skis and for other watercraft; but even if, for example, the average jet ski was used twice as much as other boats, jet skis would still have exceeded other watercraft in accident propensity per hour of use by six-fold.(33)
As for fatalities, just over 10% (84) of 821 recreational boating deaths in 1997 were to users of jet skis. (Interestingly, 74% of jet skier fatalities — triple the rate for other boater deaths — involved causes other than drowning, such as blunt trauma.(34) ) Unfortunately, the Coast Guard records only the craft used by the deceased; thus, its jet skier fatality figure omits (and mis-characterizes) cases in which a jet ski caused a fatality to a person on another vessel or to a swimmer.
As that danger has grown with the proliferation of jet skis, many paddlers, swimmers and others have had to modify or end their use of public waters and beaches. Those who remain in the water when jet skis are around now find themselves in the position of pedestrians crossing a busy street rather than carefree aquatic recreationists. This loss of amenity is difficult to quantify but is surely considerable.
Jet skis also wreak more damage to the marine environment than other powerboats. Their high speeds can be lethal to fish and marine mammals, and they discharge much of their fuel unburned into the water (see above). These impacts are magnified when jet skis venture into coves and inlets, where wildlife thrive, since toxic hydrocarbons become concentrated in the shallow waters. And of course, jet ski noise frightens shorebirds and other wildlife from their habitat, further disrupting shore ecosystems. None of these costs have been estimated, to our knowledge; nor do they lend themselves to the type of cost accounting that we have applied here to jet ski noise.(35)
DROWNING IN NOISE 57
Anderson, C.M.B. & Robinson, D.W. 1971. “The Effect Of Interruption Rate On The Annoyance Of An Intermittent Noise,” NPL Acoustics report Ac 53, National Physical Laboratory, Dept. of Trade and Industry, United Kingdom.
Anderson, R. & Wise, D. 1977. The Effects of Highway Noise and Accessibility on Residential Property Values, DOT-FH-11-8841, NTIS.
Bluewater Network. 1998. Personal Watercraft (PWC) Are Inappropriate for the National Park System (comments on the National Park Service’s proposed PWC regulations), November 13, www.earthisland.org/bw.
Bombardier Marine Products Division. 1997. Press release, “Bombardier Announces Quieter Watercraft for 1999,” September 16. Bombardier Motor Corporation of America, Melbourne, FL.
Bombardier Motor Corporation of America, Sea-Doo/Ski-Doo Division, Brand Planning/Marine Products. 1996. Set of 20 viewgraphs dated 7/30/96, summarizing a survey commissioned by the Personal Watercraft Industry Association, conducted by Bowe Marketing Research.
California Air Resources Board. 1998. Notice of Public Meeting [for December 10, 1998] to Consider Approval of California’s Pleasure Craft Exhaust Emissions Inventory, downloadable from www.arb.ca.gov as MSC9834.pdf.
Cowan, J.P. 1994. Handbook of Environmental Acoustics, Van Nostrand Reinhold, New York, NY.
Delucchi, M.A. & Hsu, S. 1996. The External Damage Cost of Direct Noise From Motor Vehicles, UCD-ITS-RR-96-3 (14). Davis, CA: Institute of Transportation Studies, University of California.
Delucchi, M. & Hsu, S. 1998. The External Damage Cost of Noise Emitted From Motor Vehicles, J. of Transportation and Statistics, Vol. 1, No. 3, pp. 1-23, October.
Fay, T.H., ed. 1991. Noise & Health, New York Academy of Medicine, New York, NY.
Feitelson, E. I., Hurd, R. E., & Mudge, R.R. 1996. “The Impact of Airport Noise on Willingness to Pay for Residences,” Transportation Research D, Vol. 1, No. 1, pp. 1-14.
Hubbard, H. & Lassiter, L. 1952. “Some Aspects of the Aircraft Noise Problem,” Aeronautical Engineering Review, I.A.S., 28-33.
McConnell, K.E. 1977. “Congestion and Willingness to Pay: A Study of Beach Use,” Land Economics, 53: 185-195, May.
McConnell, K.E. 1990. “Double Counting in Hedonic and Travel Cost Models,” Land Economics, 66(2): 121-127.
DROWNING IN NOISE 58
McCubbin, D.R. & Delucchi, M.A. The Social Cost of the Health Effects of Motor-Vehicle Air Pollution, UCD-ITS-RR-96-3 (11). Davis, CA: Institute of Transportation Studies, University of California.
National Marine Manufacturers Association, 1987. Powerboat Sound Level Engineering Report, October 16.
National Marine Manufacturers Association, Boating 1998 http://www.nmma.org/facts/boatingstats/statistic98.html.
Nelson, J.P. 1978. Economic Analysis of Transportation Noise Abatement, Ballinger, Cambridge, MA.
Nelson, J.P. 1982. “Highway Noise and Property Values: A Survey of Recent Evidence,” Journal of Transport Economics and Policy, 16: 117-138.
Nelson, P.M. 1987. Transportation Noise Reference Book, Butterworth & Co., London.
New York Times. 1995. “Watercraft Stir a Mix of Irritation and Thrills,” August 27.
New York Times. 1996. “In Puget Sound, a County’s Prohibition on Jet Skis is Overruled,” October 6.
New York Times. 1998. “Florida Keys Restricting Use of Noisy Personal Watercraft,” June 22.
New York Times. 1998. “U.S. Refuses to Ban Jet Skis at 25 Parks,” September 16.
Noise Pollution Clearinghouse, various articles on website, http://www.nonoise.org.
Noise Unlimited Inc. 1995. Letter to NJ Division of State Police, Marine Law Enforcement Bureau, November 1.
Personal Watercraft Industry Association. 2000. Website, especially http://www.pwia.org/SetSound.htm
Polaris Industries. Undated. Press release, “Polaris Genesis Watercraft Introduces Breakthrough New Technology — Quietly,” Minneapolis, MN.
Polaris Industries. 2000. Personal communications, February.
Robinson, D.W. 1971. “Towards A Unified System of Noise Assessment,” J. Sound Vib. 14 (3), 279-298.
Robinson, D.W. 1972. “An Essay In The Comparison Of Environmental Noise Measures And Prospects For A Unified System,” NPL Acoustics report Ac 59, National Physical Laboratory, Dept. of Trade and Industry, United Kingdom.
DROWNING IN NOISE 59
Robinson, D.W. 1977. “Practice And Principle In Environmental Noise Rating,” NPL Acoustics report AC 81, National Physical Laboratory, Dept. of Trade and Industry, United Kingdom.
Ross, M. et al. 1995. Real-World Emissions from Model Year 1993, 2000 and 2010 Passenger Cars, American Council for an Energy-Efficiency Economy, Washington, DC.
Ross, M. (Univ. of Michigan). 1999. Personal communication, September.
Saluck, L. (Bombardier Motor Corp.) 1999. Personal communication, February.
Silberman, J. & Klock, M. 1988. “The Recreation Benefits of Beach Renourishment,” Ocean & Shoreline Management, 11: 73-90.
Silberman, J., Gerlowski, D.A., & Williams, N.A. 1992. “Estimating Existence Value for Users and Nonusers of New Jersey Beaches,” Land Economics, 68(2): 225-236.
Time. 1999. “The 100 Worst Ideas Of The Century.” June 14.
U.S. Coast Guard, Boating Statistics 1997, http://www.uscgboating.org/stats.html.
U.S. National Park Service, 1998. Proposed Rule, Personal Watercraft Use Within the NPS System, June 12.
Verhoef, E. 1994. “External Effects and Social Costs of Road Transport,” Transportation Research A, 28A(4): 273-287.
Wagner, K.J. 1994. “Of Hammocks and Horsepower: The Noise Issue At Lakes,” LakeLine, June.
Wagner, K.J. 1999. Personal communications, January, September, December.
Wall Street Journal. 1997. “Past the Crest: Backlash Beaches Water-Bike Craze,” September 5.
Wall Street Journal. 1998. “Made in the Shade: Italy’s Bagnini Draw a Line in the Sand,” August 3.
Walsh, R.G., Johnson, D.M., & McKean, J.R. 1992. “Benefit Transfer of Outdoor Recreation Demand Studies, 1968-1988,” Water Resources Research, 28 (3), 707-713, March.
Watercraft World. 1996. “Sound Waves: Even Quieter PWC,” by Julie Filatoff, September.
Yamaha Watercraft Group, Undated. Press release, “Yamaha Debuts Noise Reduction and Emissions Control Systems with 1999 Waverunner Watercraft Line,” Yamaha Motor Corp., U.S.A., Cypress, CA.
DROWNING IN NOISE 60
This Appendix presents a complete description of the authors’ Jet Ski Noise Cost Model, beginning with what we call the Single-Beach Model (Part 1), and progressing to “Beach Type” Aggregate Models (Part 2). It also includes detailed discussions of key issues and parameters, including: · Jet ski source noise levels, both in and out of the water (Part 3) · Beachgoer utility, including its estimation from either “consumer surplus” or beach-related expenditures (Part 4) · The Noise Depreciation Index relating increased noise levels to reduced beachgoer enjoyment (Part 5) · Jet ski use taxes (Part 6) · Errors and Sensitivity (Part 7) · and Model Implementation Details (Part 8).
Part 1. The Single-Beach Model
We consider a specific beach/jet ski case for analysis, defined by ten “individual beach” parameters that describe the beach, jet ski, and beachgoers: (i) the beach’s length (along the shoreline), (ii) the beach’s depth (the distance from the shoreline to the back of the beach), (iii) the beachgoer population density and (iv) the beach’s background noise level, (v) assuming a single jet skier, his distance from shore and (vi) the noise level at the source, (vii) the “out of water” increment (how much louder the jet ski is when it briefly jumps out of the water, (viii) the “out of water” time (the fraction of the time the jet ski is out of the water, (ix) the “mean beachgoer utility,” i.e., the average value that the beachgoer attaches to his or her day at the beach, and (x) a “Noise Depreciation Index” (NDI) that describes the rate at which unwanted noise degrades the individual beachgoer’s utility.
Typical values for a hypothetical “popular lake” case might be, respectively, beach length 700 feet by depth 40 feet, a population density of one beachgoer per 100 square feet, a 65 dBA background noise level, a jet ski operating at a distance of 400 feet from the beach, generating noise at 80 dBA (at the source), increased by 15 dBA (to 95 dBA) when it jumps out of the water or employs other rapid maneuvers, which it does 20% of the time, and an average beachgoer utility of $10 per person, which degrades by 1.0% for each additional dBA of jet ski noise.
The purpose of the Single-Beach Model is to estimate the total disutility (aggregated over all beachgoers) due to jet ski noise. In the case just specified, the Single-Beach Model will estimate this total disutility to be $123 per day, assuming the jet ski operates for 3 hours over the course of the day.
DROWNING IN NOISE 61
The beach is assumed to be linear (not curved, as in a cove) — a rectangle bounded by the shoreline at the length and depth dimensions specified. The number of beachgoers is calculated from the beach’s rectangular area and population density. Each beachgoer is assigned a location on the beach, evenly spaced along the length of the beach, and randomly located as to distance from the shoreline.
For each beachgoer, we calculate the Pythagorean distance to the jet ski, keeping track of how much of the distance is over water and how much is over land. These distances are applied to a noise-level-attenuation model to obtain the jet ski noise level at each beachgoer’s location. This noise attenuation model assumes “power law” attenuation (discussed below) beyond the 20-foot distance from the jet ski at which source noise levels are measured. (At this distance of 20 feet, we assume the noise level to be 80 dBA when the jet ski is in the water and 95 dBA when it is out of the water.)
The simplest possible form of such a power law is that of an inverse square (inverse second power) rate of attenuation, or equivalently, that each doubling of the distance leads to a drop in noise level by 6 dBA. This is the law that would obtain in the case of fully 3-dimensional spreading of sound, equally in all directions. However, there is empirical evidence that for watercraft engines, the noise has a tendency to be channeled along the surface, perhaps due to reflection off the water surface, or the noise being generated underwater and/or conducted underwater, or thermal inversions.
Thus, the drop in noise level (for a doubling of distance) is somewhat less than 6 dBA. This drop in noise level is still greater than it would be for a fully 2-dimensional model (like surface water waves), for which each doubling of distance would lead to a drop of just 3 dBA (an inverse first power law). In our noise attenuation model, we assume a two-part power law, such that noise level attenuates at 5 dBA per distance doubling over water, and at 6 dBA per distance doubling over land.(36)
There is also the possibility of an additional exponential attenuation due to frictional and viscous forces, which is usually frequency-dependent. This attentuation, however, does not appear to have a significant influence on the distance scales considered here, and so we have not included it in the present model.(37)
To obtain the total noise heard by the beachgoer including that due to the jet ski, we combine this beachgoer’s jet ski noise level (“logarithmically;” see Fig. #3 in Section 4) with the beach’s intrinsic background noise level. An additional consideration is required by the variation of the jet ski noise when it jumps out of the water. The previous computation is repeated, using the higher noise level that is
DROWNING IN NOISE 62
generated when the jet ski is out of the water, and the results are applied to Robinson’s Formula (see Fig. #5 and the sidebar on p. 21) to produce an “effective” noise level.
From this we subtract the original background noise level — the noise that would obtain in the absence of the jet ski. The difference represents the additional noise experienced by the beachgoer due to the presence of the jet ski. For each beachgoer, this additional noise must be converted into disutility (dollar) units. To do this, we multiply the additional noise by the NDI to obtain the fractional degradation of the beachgoer’s enjoyment of his day at the beach.
Finally, the beachgoer’s utility in the absence of the jet ski is estimated; we assume it is statistically distributed as a doubly triangular density (here defined to be continuous and piecewise linear, with support between a minimum of zero and a maximum of twice the mean, and symmetric about the mean ), centered at the value of the mean beachgoer utility parameter. Multiplying it by the fractional degradation calculated above yields the individual beachgoer’s loss of utility. This is summed over all beachgoers (and then multiplied by 0.67; see the “Duty Cycle” discussion beginning on p. 28) to yield the total noise annoyance cost from the jet ski, for the beach in question.
Part 2. Aggregate Models and “Monte Carlo” Simulation
In an Aggregate Model, many (hundreds or thousands of) beaches of the specified type(s) are constructed according to its “beach type” parameters. The noise annoyance costs for each beach are estimated using the Single-Beach Model, and the results are aggregated statistically to produce the mean and standard deviation of the ensemble noise costs. Many of the “individual beach” variables are chosen randomly in accordance with the beach type parameters.
Let us consider beaches of the “popular lake” beach type. To construct the beaches in this Aggregate Model, values of individual beach variables are chosen randomly, as follows. The beach length is chosen randomly according to a uniform density between the values of the popular lake minimum length (80 feet) to the maximum length (800 feet); and similarly for beach depth. The jet ski noise level is also chosen randomly, according to a normal density defined by the given noise mean and standard deviation (see Part 3, below).
The jet ski distance from shore is selected according to a more complex formulation, using two “triangular” probability densities, as follows. We define a triangular probability density (characterized by two parameters, Min and Max, with Min < Max), to be a piecewise linear density
DROWNING IN NOISE 63
supported between Min and Max, with its mode at Min and with density decreasing linearly to zero at Max. For any beach, we first select a maximum possible distance M from shore for the jet ski, from a triangular density with parameters Min = 1000 feet and Max = 2,500 feet (10,000 feet for ocean beaches). (M represents such limits on jet ski distance as the far shore of a lake.)
We then select the jet ski’s distance from shore from a second triangular probability density with parameters Min = 50 feet, and Max = M, which reflects the fact that jet skiers tend to operate close to shore rather than very far away. Note that our model assumes that for any particular (simulated) beach, the jet ski remains a constant distance from the shore. In actual fact, this assumption is violated, causing still additional noise level variation, and hence additional disutility (via the Robinson effect) that is not accounted for in our model. Other reasonable probability densities could also be used.
Part 3. Noise Levels
The jet ski is assumed to have a basic noise level, which varies among jet skis as a normal random variable. We used 80 dBA at a distance of 20 feet as the noise mean (see sidebar on next page), with a standard deviation of 4 dBA. To account for moment-to-moment variation in jet ski noise, we assumed that the instantaneous noise level was always at one of two levels: the basic level defined above (when the jet ski is in the water), and a level 15 dBA louder (jumping out of the water) for 20% of the time. We then applied these “variation” parameters (and assumptions) to Robinson’s Formula to calculate the “effective” jet ski noise level, reflecting the variation between basic and elevated noise levels.
Jet skiers sometimes ride in groups; we estimate that the mean number of jet skis at a location with any jet skis is 1.6. This consideration enters into national estimates of jet ski noise costs in Section 6, since clustering of jet skis reduces the number of affected beaches. On the other hand, clustering boosts the jet ski noise level at the source by just over 2 dBA.
How loud, and how disturbing, the jet ski is, depends critically on the background noise level at the beach, without the jet ski. For a secluded lake, with few people to make noise and little or no wave action, we estimate the background noise level to be 45 dBA. For a typical popular lake beach, we estimate that the variety and density of human sounds — laughing, shouting, ball-playing, radios, lifeguard flags flapping, etc. — produces a background noise level 20 dBA higher, or 65 dBA.
Both of these values are consistent with estimates of environmental noise levels in standard acoustics references, as well as sound level
DROWNING IN NOISE 64
|
Jet Ski Source Noise Levels |
|
The most careful and, we believe, authoritative measurements of jet ski noise levels were conducted in 1993 by Dr. Kenneth J. Wagner, a limnologist and “certified lake manager,” on Watchaug Pond in Rhode Island. Dr. Wagner published his results the next year in a widely cited article in LakeLine magazine and later interpreted them for us in a series of telephone conversations and e-mails.(38) Over the course of two summer weekends, Dr. Wagner put two dozen jet skis through a range of speeds and maneuvers while he measured their sound levels at varying distances calibrated to a grid of buoys. The band of measured noise levels followed what Dr. Wagner called “an expected pattern, with variability due to both measurement error and environmental background effects.” A graph in his article relating sound levels to distances shows a range of 80-100 dBA for readings taken at 10 feet, and 75-95 dBA for readings at 20 feet. Dr. Wagner explained to us that the lower half of the observed range at 20 feet, 75-85 dBA, pertains to full-throttle operation in the water, while the high end, 95 dBA, applies to out-of-water operation. We chose the midpoint of the 75-85 dBA range, 80 dBA, to represent the noise level at 20 feet for in-water operation, with a 15 dBA increment when the jet ski is jumping out of the water. Dr. Wagner also estimated that jet skis leave the water one-fifth of the time, on average, a rate that comports with our observations. Leaving the water can be the result of deliberate “wake-jumping” or simply the natural concomitant of piloting a short-hull vehicle at high speed over even small waves. The present trend toward higher-horsepower machines noted in Section 8 suggests that Dr. Wagner’s measurements remain valid (or perhaps even low) for today’s jet ski fleet. Other measurements in the literature also suggest that a mean in-water jet ski noise level of 80 dBA is conservative. Adjusted to our convention of a 20-foot distance, a jet ski industry working group reports that older jet ski models tested as loud as 90-93 dBA in the water; for newer models, the group said only that virtually all of them tested below 84-87 dBA, implying that an average of 80 dBA for in-water use may be on the low side. The industry group also acknowledged that modifications to engine and exhaust systems can increase noise levels by 10 dBA or more, and that these “seem far more common [on jet skis than on] most other types of boats.”(39) Similarly, readings of two jet skis running in the water at full-throttle, performed for the New Jersey State Police in 1995, equate to 82-83 and 87-88 dBA at 20 feet.(40) |
measurements we have made ourselves. For intermediate beaches, we used the average of the two noise levels, yielding a background level of 55 dBA. We have used a background noise level of 65 dBA for all ocean beaches, which are generally noisier due to surf and wind.
Part 4. Beachgoer Utility and Population Density
The beachgoer utility mean represents the mean absolute utility of the day at the beach for the individual beachgoer, per person, expressed in
DROWNING IN NOISE 65
dollars. It can be dissected into two components: the actual expenditures (money spent by the beachgoer to obtain her day at the beach: travel costs, entrance fees, excess food and lodging costs beyond what she would spend otherwise) and “consumer surplus” (the additional enjoyment experienced by the beachgoer beyond her actual monetary costs). Indeed, the beachgoer’s enjoyment must be greater than (or at least equal to) her actual costs, or, as a rational economic being, she wouldn’t go to the beach.
Economic utility is usually estimated in one of two ways, each based on these two components. One way involves estimating the consumer surplus, based on “contingent valuation” or “willingness to pay” surveys (asking, “For how much money would you be willing to forego a day at the beach?”); the other way involves estimating the actual expenditures, based on surveys of travel costs. Given values for either one of these two components, and making additional assumptions of ”constant demand elasticity” and an estimate of the numerical value of this demand elasticity, one can estimate the other component and hence the total utility of the beach day.
We specify the demand elasticity of beachgoing to be 2.0, an assumption we consider conservative (i.e., low, so as to underestimate jet ski noise annoyance, at least in the standard case in which the basic component used for analysis is the consumer surplus and not the actual expenditures). Estimates in the literature indicate values at about 2.2. In addition, as a “luxury” or discretionary activity, beachgoing should have an elasticity greater than 1, and a “minimum entropy” approach would suggest that, in the absence of other information, a number known only to exceed 1 should be taken to equal 2, the harmonic mean value.(41) As a consequence, estimates of consumer surplus (or, for that matter, actual expenditures) must be doubled to estimate the total beachgoer utility mean (see sidebar, p. 66).
Estimates of beachgoer utility are available in the literature on the economics of recreation. (All values given here have been adjusted to 1999 dollars, per person per day, and have been converted from actual expenditures or consumer surpluses to total beachgoer utility by doubling, as described above.) One study, based on surveys of beachgoers’ willingness to pay for beach recreation in Rhode Island, produces estimates of $9 for a popular beach, $24 for an intermediate beach, and $26 for a secluded beach.(42) Another study, based similarly on surveys of beachgoers in New Jersey, produces estimates of $12 for what appear to be popular and intermediate beaches.(43)
Based on these two studies, we have specified values for total individual beachgoer utility mean of $10 for a popular beach, $20 for an intermediate
DROWNING IN NOISE 66
beach, and $30 for a secluded beach. To model variation among beachgoers’ valuations of the beach day, we assume that beachgoer utility is distributed according to a doubly triangular density (defined to be continuous and piecewise linear, with support between a minimum of zero and a maximum of twice the mean, and symmetric about the mean). (To substitute other values, see Part 7 of this Appendix.)
Note that a more recent “meta-analytic” study of outdoor recreation cites eleven studies of the value of a day of swimming (based on both consumer surplus and actual expenditures), and presents a computed mean of approximately $70.(44) This seems high for our purposes, though it may be consistent with widespread depictions of beachgoing in popular culture, advertising, etc. as Americans’ quintessential leisure experience, and one to which participants attach a high value.
|
Elasticity of Demand for Recreation |
|
A ”demand curve” is of the form P = P(Q), where Q is the quantity of a commodity demanded by consumers, and P is the highest (per item) price at which the quantity Q will be demanded by consumers. Here P is expressed as a function of Q, although it is probably more intuitive to think of the demand quantity Q as depending upon the price P rather than the reverse; however, the present convention is nearly universal and much more useful in economics. P(Q) is always a monotone decreasing function, and is concave upwards. The ”elasticity” (at any point of economic equilibrium) is the small-perturbation limit of the relative change in demand as a result of a relative change in price. That is, if the elasticity equals, say 2.4, a 1% increase in price will cause a 2.4% decrease in demand. ”Luxuries” are usually characterized by elasticities greater than one, and “necessities” by elasticities less than one. Although the demand elasticity for a single commodity can vary greatly over different price regimes, it is often assumed (somewhat as a convenience to economic analysis, but generally with decent empirical validity) that the elasticity is constant over a wide range of prices. It is not hard to show that if constant elasticity is assumed, then the demand curve must be of the “power law” form P(Q) = K x Q - (1/ E), where E is the (constant) elasticity and K is a constant.(45) At market equilibrium ( P0(Q0), Q0 ), the total actual expenditures (AE = P0 x Q0) and the total consumer surplus (CS = integral ((P(Q) - P0) dQ, Q = 0 to Q0 )) are in a fixed ratio depending only on the elasticity, and are therefore estimable from each other. This relation is given by AE = CS x (E - 1), so that the total utility = AE + CS = CS x E. This result depends on a ”luxury” assumption that the elasticity exceeds 1; if the (constant) elasticity is less than 1, the consumer surplus is infinite. Beachgoing (and recreation demand in general) satisfies this ”luxury” assumption, since the elasticity appears to be around 2. This relation between AE and CS pertains to ensemble utility across all beachgoers; by averaging over beachgoers, the relation extends to individuals. |
DROWNING IN NOISE 67
We drew our beachgoer population densities largely from our observations of hundreds of beaches of all types (lake, bay, river and ocean) in every part of the United States over several decades. Our value for popular beaches, one person per 100 square feet of beach, corresponds to federal standards promulgated in the 1970s, of 75-100 square feet per person.(46) Italian beaches are reported to be several times more crowded.(47)
At the other extreme, our value for secluded beaches of one person per 10,000 square feet implies that a 1000-foot long ocean beach averaging 200 feet from shore to rear would have just 20 people, or a half-dozen or so groups of 2-4 each. While this is more people than at a classic (or fantasy) “deserted” beach, it appears to fit the common notion of “seclusion” in modern-day America.
Part 5. Noise Depreciation Index (NDI)
The Noise Depreciation Index is a numerical measure of the degree to which additional noise in an environment degrades its utility value. The estimate we have used here is 1.0% per dBA, indicating that for “K” additional dBA’s of effective noise level, the beachgoer’s utility declines by 0.01 x K x her previous utility.
The literature contains no studies of beachgoers’ willingness to pay for quiet. However, the concept of an NDI is well established with respect to transportation noise. Delucchi and Hsu, in an exhaustive review of motor vehicle and airport noise costs, noted that empirical studies of reductions in housing value associated with noise level have reported NDI’s ranging from 0.2% to 1.3%.(48) However, Delucchi and Hsu also noted that much higher NDI estimates have been reported in so-called contingent-valuation studies, which assess peoples’ “willingness to pay” to avoid highway or airport noise.
One such recent study by Feitelson et al. surveyed several thousand people in three communities near a large airport where a major expansion was planned. Respondents were asked what they would pay to buy or rent a residence in an area with no aircraft noise, and the same hypothetical residence in areas with different levels and frequency of noise exposure. From their responses, the authors inferred an NDI range of 2.4% to 4.1% for home owners, and 1.8% to 3.0% for renters. That is, for each decibel of noise they would avoid, home owners were willing to pay between 2.4% and 4.1% more in house prices, and renters were willing to pay 1.8% to 3.0% more in rents.(49) The mean value of these ranges is 2.8%, indicating an NDI for airport noise of almost 3%.
Other contingent-valuation studies cited by Delucchi and Hsu have also reported NDI results several times higher than those estimated in
DROWNING IN NOISE 68
the earlier empirical studies of actual property values. The key reason for the difference, as Delucchi and Hsu note, is that some of the empirical studies estimated only the loss of market value, and not the full loss of use value. As we have noted in discussing “consumer surplus” (in Section 4 and in Part 4 of this Appendix), what one actually pays for an item is only a lower bound for one’s valuation of it. Accordingly, the contingent-valuation approach, as employed by Feitelson and others, would be more likely to capture the full extent of lost utility in housing from environmental noise.
However, there are a number of differences between Noise Depreciation Indexes for highway and airport noise, on the one hand, and for jet skis on the other. Transportation values are based on a 24-hour equivalent sound pressure level, whereas a 24-hour average is irrelevant to beachgoers who may spend only 3 hours of their leisure time at the beach. Highway noise levels also tend to create a more uniform noise, without the variations that characterize jet ski noise. In addition, beachgoers generally do not own the lakefront or oceanfront property they are using. Finally, property value loss and the lost value to beachgoers are related but not identical matters.
In consideration of the higher estimates from contingent-valuation studies, and to account for both the importance of aesthetics to beach recreation and the differences between transportation noise and jet ski noise, we have selected a value of 1.0% to represent the NDI from jet ski noise to beachgoers during periods when a jet ski is present.
Part 6. Jet Ski Use Taxes
The effect of a change in price on demand for a service or product can be approximated through the formula Q1/Q0 = K x (P1/P0)-E, where K is a constant, Q0 and P0 are the current quantity and price of the product; Q1 and P1 are the altered quantity and price; and E is the elasticity, which we defined in the sidebar on p. 66 as the small-perturbation limit of the relative change in demand as a result of a relative change in price.
We assume an elasticity of 2.2 for jet skiing. As noted in Part 4, the estimated elasticity of beachgoing is probably around 2; jet skiing, as a somewhat more discretionary or luxury activity, should have a higher price-sensitivity or elasticity.
We further estimate that it costs an average of $1,700 a year to own and operate a jet ski; this is predicated on an average purchase price of $6,000 with a straight-line amortization over eight years (yielding an annualized purchase price of $750),(50) annual costs of $250 each for storage, hauling
DROWNING IN NOISE 69
and maintenance, and close to $200 a year for fuel (calculated on 15 days of use, 9 gallons per day,(51) and $1.35/gallon).
An annual tax on jet skis of $700, equivalent to the average jet ski’s noise costs to beachgoers, would add 41% to this annual $1,700 cost. Substituting 1.41 for P1/P0 in the formula above, with E = 2.2, yields 0.47 for Q1/Q0, indicating that the tax would lead to a 53% reduction in demand (usage). Similarly, a tax rate of half of the amount of noise costs, or $350, would amount to a 21% rise in the annual cost of owning and using a jet ski; a value of 1.21 for P1/P0 yields 0.66 for Q1/Q0, indicating that a 34% reduction in demand would be associated with this lower tax.
Part 7. Errors and Sensitivity
Although many of our input parameter values and other assumptions must be regarded as educated — or rather, well-educated — guesses, we believe they are reasonable. Approximations are inherent in any economic estimation of this type, and ours appear to yield reasonable “order of magnitude” results. We believe that the accuracy of our results is high for Single-Beach Models (for which the beach can be characterized precisely), somewhat less so for Aggregate Models (like “popular lake” or “national,” for which characterization is necessarily imprecise).
However, the accuracy is very good for sensitivity analysis, making our model quite reliable at gauging the effectiveness of mitigation strategies. Indeed, sensitivity analyses provide more robust results than the Aggregate Models upon which they are based. Whatever inaccuracies may be present in the Aggregate Models as absolute disutilities (first order), are significantly smaller as relative disutilities (second order).
Two parameters that particularly warrant further study are the beachgoer utility means and the NDI. Is it reasonable that a beachgoer’s utility (per day) is the $10/$20/$30 we use in this report? We believe so, but there is evidence that these figures are too low by a factor of 2 or more (see Walsh, 1992). Since most model outputs are linear in the mean utility, readers who wish to see how our model results would change from specifying a higher daily beachgoer utility, can multiply our model results by the appropriate factor of 2 or more. (Not all outputs are linear, however; doubling the beachgoer utility would double the total national disamenity, but not, say, the fraction of waters from which jet skis must be banned to halve the national noise disamenity.)
Similarly, most model outputs are linear in the NDI. That is, readers who prefer a factor of 2.0%, or 0.5%, to our value of 1% don’t need to re-run the model, but can simply double or halve our results as appropriate. This holds as well for our duty cycle factor of 0.67; where
DROWNING IN NOISE 70
the jet ski is present for, say, 85% of the beachgoer’s time, rather than 67% as we assumed, our model results would increase proportionally.
Part 8. Model Implementation Details
The models underlying the analysis in this report were implemented in the Fortran programming language. They may be run on a standard Pentium (or later) PC with a Fortran compiler. Run times range from less than a second for single-beach models to as much as several hours for multiple mitigation-factor analyses.
Those interested in obtaining and running the model should contact the Noise Pollution Clearinghouse using our web form, by mail at P.O. Box 1137, Montpelier, VT 05601, or by calling toll-free 1-888-200-8332.
(1) A jet ski is a vessel, usually less than 16 feet in length (measured from end to end over the deck excluding sheer) which uses an inboard, internal combustion engine powering a water jet pump as its primary source of propulsion. The vessel is intended to be operated by a person or persons positioned on, rather than within, the confines of the hull. Jet skis are high-performance vessels designed for speed and maneuverability and are often used to perform stunt-like maneuvers. (Adapted from U.S. National Park Service, 1998).
(2) All terms such as “noise costs” and all findings are explained and derived in the text, particularly in Sections 3 through 6.
(3) That is, the opposite of amenity; the reduction or destruction of what would otherwise be an amenity.
(4) Due to legal considerations, the Lake Tahoe ordinance was drafted to ban all two-stroke engines rather than just jet skis. It permits two-stroke engines as an ancillary power source (for sailboats), or engines that use electronic fuel injection meeting advanced federal and state air emission standards, or that are less than 10 horsepower (the latter through Oct. 31, 2001 only).
(5) Arbitrarily characterizing a lake as an ellipse twice as long as it is wide, a 300-acre lake is roughly 5,770 feet long and 2,885 feet wide. Under the Vermont rule, then, lakes under half a mile across are off-limits to jet skis.
(6) The Monroe County ordinance applies to 14 beaches from Key West to Key Largo, and limits speeds to 5 mph until jet skis reach a distance of 1200 feet. (New York Times, 1998)
(7) See Personal Watercraft Industry Association (2000), for example.
(8) Bluewater Network, 1998, p. 28.
DROWNING IN NOISE 71
(9) Their relative magnitudes depend on the “demand elasticity”; for a detailed discussion see the sidebar “Constant Demand Elasticity” on p. 66.
(10) An alternative approach, discussed in Part 4 of the Appendix, involves estimating consumer surplus, based on “contingent valuation” surveys that ask, essentially, “For how much money would you be willing to forgo a day at the beach?”
(11) The California Air Resources Board estimates that the average jet ski is operated for 41 hours a year. (CARB 1998, Tables 6 and 7) We assume that the average jet ski is used 3 hours a day on 15 days a year, or 45 hours a year.
(12) If the jet skier and the beachgoer each spend their three hours distributed randomly and independently over the assumed six-hour beach day, the beachgoer would have the jet ski’s presence half of the time. A more likely scenario is that each would spend their respective three hours as a contiguous block of time. Assuming that the timing of these blocks is distributed uniformly and independently of each other, a probabilistic computation indicates that the beachgoer will have the jet ski’s presence two-thirds of the time.
(13) While “centering” the jet ski’s lateral position is a “worst case” assumption (i.e., it maximizes total beachgoer exposure to the noise), it is plausible or even likely. Moreover, its non-conservatism is partially offset by distributing beachgoers evenly between the shoreline and the back edge of the beach in our model, rather than concentrating them more realistically closer to shore.
(14) The 2.04 dBA increment is derived as 10 x log (1.6). This calculation is conservative since it assumes identical sound profiles for each jet ski in a cluster.
(15) At 44¢, the per-person noise cost at this beach is slightly less than the 50¢ shown in Table 3 for a popular ocean beach. This is because average distances from the jet ski are greater at this huge beach.
(16) The National Marine Manufacturers Association (1998) estimated the number of jet skis in use to be 1.0 million in 1997 and 1.1 million in 1998, suggesting 1.2 million in 1999 and a current (2000) figure of 1.3 million, based on annual sales of 150,000 units and estimated scrappage of 50,000. Separately, according to a survey of jet ski owners by the main manufacturer trade group (see next footnote), the average jet ski is used 7 times a month during the “riding season.” Allowing for the likelihood that survey respondents had higher than average use, we assumed an average of 15 days of use a year.
(17) Data in text are from Bombardier Motor Corporation of America (1996), p. 10 (for place of use) and p. 11 (for frequency of use). The survey was mailed to 10,500 holders of warranties from five jet ski manufacturers for jet skis purchased during 1991-95, and generated 2,800 usable responses, a reply rate of 26%. See also Saluck, 1999.
(18) To be sure, noise can impose health-related costs through cardiovascular strain, mental and emotional stress, etc. Not all of these costs are captured through our Noise Depreciation Index derived from studies of noise-related property-value loss. Jet skis in particular may also create economic losses by discouraging beach visits and non-motorized activity. These costs are beyond the scope of this report.
DROWNING IN NOISE 72
(19) Delucchi & Hsu, 1996. The authors state, “We find that the external damage cost of direct motor-vehicle noise could range from as little as $100 million per year to approximately $40 billion per year (1990 data, 1991 dollars), although we believe that the cost is not likely to exceed $5 billion.” (pp 1-2) Adding 10% to reflect growth to 1999 vehicle levels and 27% to adjust to 1999 dollars, for a combined increment of 40%, yields figures in text.
(20) Personal Watercraft Industry Association (2000).
(21) Yamaha claims that its Yamaha Sound Suppression “reduces the sound intensity level of the XL1200 Ltd. [three-person Wave Runner model] by 70 percent of last year’s XL1200.” (Yamaha, undated.) A 70% reduction in sound intensity equates to a 5.2 reduction in dBA. Bombardier (1997) and Polaris (undated) assert that their respective new SEA-DOO and Genesis product lines deliver reductions in sound pressure of 50% and 60%, respectively; these correspond to respective dBA reductions of 6.0 and 8.0. However, a spokesman for Polaris acknowledges that its new Genesis Watercraft produces a noise level of 73 dBA at a distance of 25 meters. (Polaris, 2000) Adjusted to our “reference” distance of 20 feet, this is equivalent to 83 dBA. We were unable to obtain estimates of actual noise levels for the Yamaha and Bombardier machines, despite repeated phone calls to both manufacturers. The above were the sole noise reduction claims posted on the PWIA web site.
(22) Realistically, bans would lead to a diminution of total usage. In addition, beachgoers with high noise sensitivities would gravitate to jet-ski-free beaches, while those with greater noise tolerance would tend to remain at areas where jet skis are permitted. Both phenomena would heighten the reduction in noise costs resulting from bans. Conversely, bans would have a smaller effect on national noise costs if, as we consider likely, they were applied disproportionately to smaller and/or less-frequented beaches. These considerations were beyond our analytical range here but are deserving of further study.
(23) Recall that we assume a 67% duty cycle, with a jet skier impinging on a beachgoer for two-thirds of the beachgoer’s day rather than 100%. With the “time sharing” scenario in the text, and under a worst-case assumption in which the total number of jet skis is unchanged, the duty cycle would fall, but only to one-half, making a 25% reduction from 67% (since 0.50 / 0.67 = 0.75). Note that the average size of a jet ski cluster would rise from the “base level” of 1.6, adding to the source noise level and shrinking the reduction in noise costs.
(24) One could say equivalently that assessments of jet ski noise that ignore out-of-water operation overlook 84% of the overall impact of jet ski noise.
DROWNING IN NOISE 73
(25) Even enthusiasts may suffer reduced real estate values, as jet ski noise makes their property less attractive to a large segment of potential buyers and renters.
(26) The calculation is: 2,000,000 x ½ x ½ x 7.6 dBA x $100,000 x 6% x 1.0%, yielding $228 million. The figure of 2 million beachfront houses was derived from an estimate of 60,000 lakes in the U.S., each fronted by an assumed average of 30 houses, yielding 1.8 million lakefront houses. We added 200,000 houses on rivers, bays, canals and oceans for a total of 2 million. The figure of 60,000 lakes was derived from known numbers of lakes in MN (15,000), WI (10,000), ME (5,000), and MA (1,500), plus estimates of 5,000 for MI and 4,000 for NY. Assigning roughly 20,000 to the other 44 states yields a national total of around 60,000.
(27) The added noise level from a jet ski on the open ocean is much higher than on ocean beaches, due to the absence of background surf noise. In any event, since 92% of jet ski use is on lake-type waters, the 37 dBA noise increment on secluded lakes is a good approximation of the average noise increment imposed by a jet ski cluster on sailboaters, kayakers, swimmers, etc.
(28) Walsh, 1992. The mean value of a recreation day of non-motorized boating was 112% greater than (i.e., slightly more than double) their mean value for a day of swimming, consistent with the expense associated with use of boats.
(29) The calculation is: 12.2 million x ½ x 2 x 37 dBA x $40 x 1.0% x 0.67 duty cycle factor, yielding $120 million.
(30) U.S. annual fuel use by jet skis is around 180 million gallons, based on per-jet ski daily fuel use of 9.2 gallons (PWIA survey, or Bombardier, 1996) and 19.5 million “jet ski days” estimated earlier. In comparison, U.S. motor vehicles annually consume approximately 125 billion gallons of gasoline, of which almost all in light-duty gasoline vehicles. The ratio of the respective gallon figures is around 700 to 1.
(31) McCubbin & Delucchi, 1996, Table 11.7-6. The cost range, 0.58¢ to 7.71¢, exclude visibility and ecosystem damage from air pollution (these are treated in other reports by Delucchi in the series), “upstream emissions” (e.g., from oil refining) and road dust (treated in the same report). The wide range reflects uncertainties in the rates of pollutant emission, dispersion, human exposure, and disease generation.
(32) U.S. Coast Guard, 1997. Data are from Boating Accident Reports for recreational boats. Of 5,089 vessels in collisions, 2,486 were PWC (personal watercraft, i.e., jet skis), and 310 were unknown (see p. 30); excluding the latter, jet skis were 52% of the total.
(33) Ibid., pp. 4 and 5. The Coast Guard estimated that there were 12.3 million “numbered [registered] boats” in 1997, of which 0.5 million were jet skis. However, the latter figure excluded 25 states, including some with the most jet skis (see p. 24), and is only half the 1997 figure reported by trade associations and others. We therefore added 0.5 million jet skis to the Coast Guard 1997 figures, for 1.0 million jet skis, making an 8% share of a 12.8 million total. If 8% of boats (the jet skis) were in 52% of serious accidents (see prior footnote), and the remaining 92% of boats were in 48%, then jet skis were in accidents 12.5 times as often as other boats.
DROWNING IN NOISE 74
(34) Ibid., p. 16.
(35) For a detailed description of the full range of jet ski damage to people and the natural environment, see Bluewater Network, op. cit.
(36) In 1987, the National Marine Manufacturers Association measured an average reduction in sound levels from motorboats of 4.8 decibels with a doubling of distance from 50 to 100 feet, and 5.1 decibels with a further doubling to 200 feet. (NMMA, 1987) These figures hold over a wide variety of types of powerboat with remarkable consistency (standard deviations of only 0.6 dBA in the first case and 1.0 dBA in the second). Our attenuation model is based on a noise level loss of 5 dBA per doubling of distance over water and 6 dBA per doubling of distance over land, or inverse power laws with exponents of 1.661 and 1.993, respectively.
(37) At the somewhat high-end frequency of 1000 hertz, the typical value for this additional attenuation is only 1 dBA at 4000 feet and is much less at 1000 feet. These figures increase at higher frequencies, and could be as high as 6 dBA and 2 dBA, respectively. On this basis, we conclude that exponential attenuation can be safely ignored over the distance regimes under consideration here. Hubbard, 1952.
(38) Wagner, 1994 and 1999.
(39) We quote from an uncredited, but apparently industry-based document, identified as PIANC SPN Working Group No. 6, Discussion of Personal Watercraft Noise-Related Issues, undated: “Current PWC models are virtually all below 78-80 dBA at a distance of 15 meters (50 feet) [while] older models may be as loud as 84-86 dBA and modified PWC … may be much louder [by] 10 dBA or more.” We added 6-7 decibels to these ranges to adjust from the 50-foot distance to our base distance of 20 feet.
(40) Noise Unlimited Inc., 1995. Readings were taken at 50 feet for two Kawasaki Jet Skis: model 750 STS (81 dBA) and model 900, High Performance 3 Cylinder 100 hp (76 dBA). Text figures are 6-7 dBA higher to adjust for difference in reference distance from our 20 feet.
(41) The usual mean and median are not defined on the infinitely long interval [1, ¥), i.e., from 1 to infinity. In this situation, a “natural” measure often used is the “harmonic” measure, which is induced by the reciprocal map y = 1/x (which maps [1, ¥) onto the “unit interval” [0, 1], with the standard “uniform” measure ). This induces the measure dy = (1/x^2) dx on [1, ¥); under this measure, the median is 2.0. The mean is still undefined on [1, ¥), although the value 2.0 corresponds to the mean 0.5 of [0, 1] under uniform measure.
DROWNING IN NOISE 75
(42) McConnell, 1977. McConnell used a semilog regression to estimate consumer surplus. We assumed values of $20K for family income (in the 1974 dollars used in his regression), air temperature of 85· F, beachgoers averaging 10 beach visits per season, and beachgoer density of 1 person per 100 square feet corresponding to a popular beach. These values yield a consumer surplus of $4.50 (adjusted to 1999 dollars), which must be doubled to derive total beachgoer utility. Assuming 5 beach visits per season instead of 10 would raise this result by one-third.
(43) Silberman & Klock, 1988. Although Silberman & Klock did not specify the population density of the beaches they surveyed, their location, on the Jersey Shore within the New York metropolitan area, suggests high usage rates. In addition, their efforts to correlate beachgoer utility to beach “congestion” were inconclusive.
(44) Walsh et al., op. cit.
(45) The “power law” equation is the solution to the “constant elasticity = E” differential equation: (dQ/Q) / (dP/P) = - E .
(46) McConnell, op. cit., reports that the federal Bureau of Outdoor Recreation’s 1974 beach standard equated to 75 square feet per person, with 100 square feet “as a more appropriate standard for environmental concern.” (pp. 191-192) McConnell also reports that Ohio, Nebraska and California promulgated standards in the early 1970s that ranged between 75 and 109 square feet per person, while Vermont recommended 25-50 square feet. (p. 192n)
(47) The Wall Street Journal, 1998, reports that Italy’s bagnini (beach workers) place beachgoers’ uniform umbrellas exactly 6 feet apart. Since each umbrella effectively commands a 6-foot square, each beachgoer occupies 36 square feet.
(48) Delucchi & Hsu, op. cit.
(49) E. I. Feitelson et al., 1996. These ranges include valuations inferred from respondents who indicated that no price or rent reduction could induce them to live in the noisier district.
(50) National Marine Manufacturers Association, 1998, reports average retail prices for jet skis of $6,328 in 1996, $6,454 in 1997 and $6,681 in 1998, suggesting that $6,000 is a reasonable estimate of the sale price of jet skis in service in 1999.
(51) Respondents to the PWIA survey (Bombardier, 1996, op. cit.) reported average daily fuel use of 9.2 gallons.
DROWNING IN NOISE 76
The Noise Pollution Clearinghouse is a national non-profit organization working to create more livable cities and more natural rural and wilderness environments by reducing noise pollution at the source. You may contact us through our web site, www.nonoise.org, using our web form, by mail at P.O. Box 1137, Montpelier, VT 05601, or by calling toll-free 1-888-200-8332.
Charles Komanoff is known internationally for deconstructing the failed economics of nuclear power, as author-researcher (Power Plant Cost Escalation) and expert witness for state and local governments. He is also prominent in the pedestrian and cyclist movement in New York City as a founder of Right Of Way, as “re-founder” of Transportation Alternatives, and as editor and author of the Bicycle Blueprint and Killed By Automobile. He consults and writes on transport pricing, traffic costs, and alternatives to road-building. Charles has a B.A. from Harvard in Applied Mathematics and Economics. He lives in New York City with his wife Judy and their two sons.
Dr. Howard Shaw has made a career of creating mathematical models for scientific and engineering phenomena and implementing them in computer-based forms. He has worked in industry as a Professional Engineer and Systems Analyst in a wide range of areas including acoustics. He is a Full Professor of Computer Science and Mathematics at the Western State College of Colorado in Gunnison, and has taught at the University of Massachusetts in Amherst, and at the University of Michigan in Ann Arbor. Dr. Shaw has a B.S. in Mathematics from MIT and a Ph.D. in Mathematics from the University of Michigan. He and his wife Cheryl live in Gunnison.
The authors gratefully acknowledge the Noise Pollution Clearinghouse for financial support · graphic design of the report and cover by Phyllis · illustrations by Margarita Suarez · the penetrating editorial, analytical and presentation guidance of Katie Alvord, Mark Delucchi, David Morris, John Plunkett, Vince Taylor, Ken Wagner and, particularly, Les Blomberg and Michael J. Smith · helpful reading of early drafts by Jeff Anzevino, Arline Bronzaft, Roger Cox, Steve Dunn, Kenneth Foreman, and Cheryl Jackson Hall.
![]()